Question

An object is thrown vertically upward from a height of 2m at $7m{{s}^{-1}}$. How long will it take for the object to hit the ground?

Answer 1

Hint: We shall analyze the velocity of the object at various points of its motion and apply the equations of motion at those points. However, before applying the equations of motion, we will first break down the journey of the object into two parts.

Complete answer:
We have marked three points in the journey of the object that are A, B and C respectively. Also, we break up the motion of the object into two parts, from A to B and from B to C.

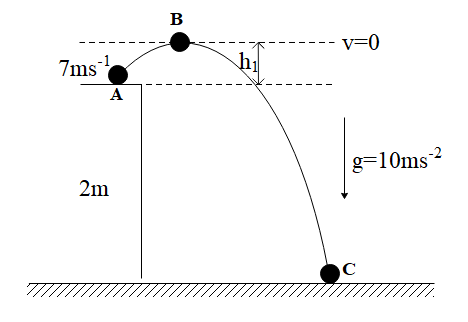
We shall first look into the motion of the object from A to B.
At point A, the object has an initial velocity of $7m{{s}^{-1}}$. When it is thrown vertically, it does not fall downwards directly rather it goes upward to reach its maximum height. At the maximum height, the velocity of the object is zero. Thus, the acceleration acting on it is negative of the acceleration due to gravity, that is,$-10m{{s}^{2}}$. Let the time taken to complete this journey be ${{t}_{1}}$.
Applying the equation of motion, $v=u+at$ and substituting values, $v=0m{{s}^{-1}},u=7m{{s}^{-1}},a=-10m{{s}^{-2}},t={{t}_{1}}$, we get
$\Rightarrow 0=7+\left( -10 \right){{t}_{1}}$
$\Rightarrow 10{{t}_{1}}=7$
Dividing both sides by 7, we get
$\Rightarrow {{t}_{1}}=\dfrac{7}{10}s$
Also, ${{h}_{1}}=\dfrac{{{v}^{2}}-{{u}^{2}}}{2a}$
$\begin{align}
  & \Rightarrow {{h}_{1}}=\dfrac{0-{{7}^{2}}}{2\left( -10 \right)} \\
 & \Rightarrow {{h}_{1}}=\dfrac{49}{20}m \\
\end{align}$
$\Rightarrow {{h}_{1}}=2.45m$
Now, when the object travels from point B to C, the object is freely falling under the force of gravity from its maximum height. Applying the equation of motion, $s=ut+\dfrac{1}{2}a{{t}^{2}}$ and substituting the values, $s=2m+{{h}_{1}},u=0m{{s}^{-1}},a=10m{{s}^{-2}},t={{t}_{2}}$ , we get
$\Rightarrow 2+2.45=\left( 0 \right){{t}_{2}}+\dfrac{1}{2}\left( 10 \right)t_{2}^{2}$
$\Rightarrow 4.45=5t_{2}^{2}$
$\Rightarrow {{t}_{2}}=\sqrt{\dfrac{4.45}{5}}s$
 Thus, the total time of motion of the object is ${{t}_{1}}+{{t}_{2}}$.
$\begin{align}
  & \Rightarrow t=\dfrac{7}{10}+\sqrt{\dfrac{4.45}{5}} \\
 & \Rightarrow t=0.7+0.94 \\
\end{align}$
$\Rightarrow t=1.64s$
Therefore, time taken for the object to hit the ground is 1.64 seconds.

Note:
In motion from A to B, we have taken the acceleration of the object as negative of acceleration due to gravity because it is going in the exact opposite of the acceleration due to gravity. However, in motion from B to C, we have taken the acceleration to be positive acceleration due to gravity because then the object is moving in the same direction as that of the acceleration due to gravity.