
An object of a mass M is attached to a vertical spring which slowly lowers to equilibrium position. This extends the spring x. If the same objects is attached to the same vertical spring but permitted to fall suddenly instead, then the maximum extension of spring is
Answer
515.1k+ views
Hint – To find the maximum extension we draw a free body diagram of the object and compute all the forces acting on it during both the cases individually. In both the cases the spring constant is the same, using this we establish a relation between both the distances.
Formula Used:
Force acting on an object of mass m, F = mg
Force on a spring F = -kx, where x is the extension of the spring
Potential energy of an object PE = mgh, where m is the mass of the object and h is the height at which it is placed.
Potential energy of a spring PE =
(g and k are gravitational constant and spring constant respectively.)
Complete step-by-step solution -
Given Data:
Mass of the object is ‘m’ and the spring is extended to a distance x when attached slowly.
When the object is attached slowly:
The free body diagram of the object looks like this:
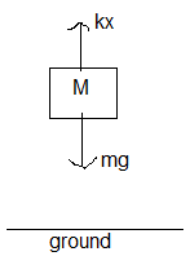
The weight of the object pulls it towards the ground and the force on spring pulls it in the opposite direction. The objects equilibrium when both forces are equal to each other.
At equilibrium all the forces acting on the body should be equal, i.e.
When the object is allowed to free fall:
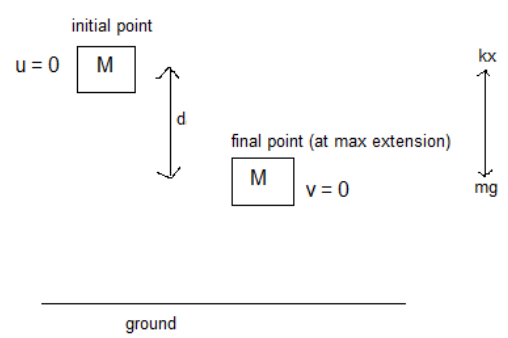
The free body diagram of the object looks like this:
When an object is let to free fall, the initial velocity of the object would be u = 0. The spring has been extended to a distance, let that be ‘d’. During the process of compressing the spring the object keeps gaining velocity but at the point of maximum compression the velocity of the object again becomes zero, i.e. final velocity v = 0.
During the entire process the object is subject to two forces only, which are the weight of the object ‘mg’ and the force due to spring ‘kx’. Both these forces are conservative forces, that means the total change in mechanical energy is zero.
⟹∆M.E = 0, when a non-conservative force does not do any work then mechanical energy remains conserved.
Now we know Mechanical energy = Kinetic energy + Potential energy
⟹∆M.E = ∆K.E + ∆P.E
In our scenario,
⟹∆K.E + ∆P.E = 0 ------------- (a)
From the figure the initial velocity of the object and final velocity of the object u =0 and v = 0, hence the change in kinetic energy becomes zero.
⟹∆K.E = 0
Substituting it in equation (a) it becomes, ∆P.E = 0 ------------ (b)
We have to compute only the change in Potential energy,
The potential energies acting upon the object are the gravitational potential energy of the object and the potential energy of the spring.
Hence from equation (b),
⟹∆P.E = 0
Gravitational potential energy is given by ‘mgh’, here our object travelled a distance d,
Therefore
And the spring is unstressed initially, then it is compressed, the PE of a spring is given by
Substitute the value of k from equation (1) in the above equation, we get
Hence the maximum extension on the spring is 2x.
Option B is the correct answer.
Note – In order to answer questions of this type the key is to know the meaning of potential energy, kinetic energy, conservative forces. Drawing a free body diagram for both the cases and finding all the forces acting on the object in each case is a crucial step.
Potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity.
A conservative force has a property that the total work done in moving a particle between two points is independent of the taken path. Equivalently, if a particle travels in a closed loop, the total work done by a conservative force is zero. A conservative force depends only on the position of the object.
Formula Used:
Force acting on an object of mass m, F = mg
Force on a spring F = -kx, where x is the extension of the spring
Potential energy of an object PE = mgh, where m is the mass of the object and h is the height at which it is placed.
Potential energy of a spring PE =
(g and k are gravitational constant and spring constant respectively.)
Complete step-by-step solution -
Given Data:
Mass of the object is ‘m’ and the spring is extended to a distance x when attached slowly.
When the object is attached slowly:
The free body diagram of the object looks like this:

The weight of the object pulls it towards the ground and the force on spring pulls it in the opposite direction. The objects equilibrium when both forces are equal to each other.
At equilibrium all the forces acting on the body should be equal, i.e.
When the object is allowed to free fall:

The free body diagram of the object looks like this:
When an object is let to free fall, the initial velocity of the object would be u = 0. The spring has been extended to a distance, let that be ‘d’. During the process of compressing the spring the object keeps gaining velocity but at the point of maximum compression the velocity of the object again becomes zero, i.e. final velocity v = 0.
During the entire process the object is subject to two forces only, which are the weight of the object ‘mg’ and the force due to spring ‘kx’. Both these forces are conservative forces, that means the total change in mechanical energy is zero.
⟹∆M.E = 0, when a non-conservative force does not do any work then mechanical energy remains conserved.
Now we know Mechanical energy = Kinetic energy + Potential energy
⟹∆M.E = ∆K.E + ∆P.E
In our scenario,
⟹∆K.E + ∆P.E = 0 ------------- (a)
From the figure the initial velocity of the object and final velocity of the object u =0 and v = 0, hence the change in kinetic energy becomes zero.
⟹∆K.E = 0
Substituting it in equation (a) it becomes, ∆P.E = 0 ------------ (b)
We have to compute only the change in Potential energy,
The potential energies acting upon the object are the gravitational potential energy of the object and the potential energy of the spring.
Hence from equation (b),
⟹∆P.E = 0
Gravitational potential energy is given by ‘mgh’, here our object travelled a distance d,
Therefore
And the spring is unstressed initially, then it is compressed, the PE of a spring is given by
Substitute the value of k from equation (1) in the above equation, we get
Hence the maximum extension on the spring is 2x.
Option B is the correct answer.
Note – In order to answer questions of this type the key is to know the meaning of potential energy, kinetic energy, conservative forces. Drawing a free body diagram for both the cases and finding all the forces acting on the object in each case is a crucial step.
Potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity.
A conservative force has a property that the total work done in moving a particle between two points is independent of the taken path. Equivalently, if a particle travels in a closed loop, the total work done by a conservative force is zero. A conservative force depends only on the position of the object.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




