Question

An oil company required 12000, 20000 and 15000 barrels of high grade, medium grade and low grade oil respectively. Refinery A produces 100, 300 and 200 barrels per day of high grade, medium grade and low grade oil respectively. While, refinery B produces 200, 400 and 100 barrels per day of high grade, medium grade and low grade oil respectively. If refinery A costs Rs 400 per day and refinery B costs Rs 300 per day to operate, then the days should each be run to minimize costs, while satisfying requirements are
A.30,60
B.60,30
C.40,60
D.60,40

Answer 1

Hint: You want to determine values of x and y such that z is minimized, subject to the given conditions. This problem involves analysis of a linear equation. You may need to solve a system of linear equations to find some of the coordinates of the points in the middle.
Let x and y be the number of days of refinery A and refinery B respectively.
The total cost $z=400x+300y$ is the linear function which is to be minimized; hence it is the objective function.

Complete step-by-step answer:
High Grade barrel
Production by Refinery A in x days = 100x
Production by Refinery B in y days= 200y
Total minimum required production = 12000

2. Medium grade barrel
Production by Refinery A in x days = 300x
Production by Refinery B in y days= 400y
Total minimum required production = 20000

3. Low grade barrel
Production by Refinery A in x days = 200x
Production by Refinery B in y days= 100y
Total minimum required production = 15000

Obviously x and y cannot be negative, $x\ge 0,y\ge 0$
Hence, the linear programming problem (LPP) is formulated as,
Minimize $z=400x+300y$
Subject to, $100x+200y\ge 12000,300x+400y\ge 20000,200x+100y\ge 15000$
$x\ge 0,y\ge 0$
Consider equations obtained by converting all inequalities representing the constraints and draw the corresponding lines.
\[\begin{align}
  & 100x+200y=12000.............(1) \\
 & 300x+400y=20000.............(2) \\
 & 200x+100y=15000..............(3) \\
\end{align}\]

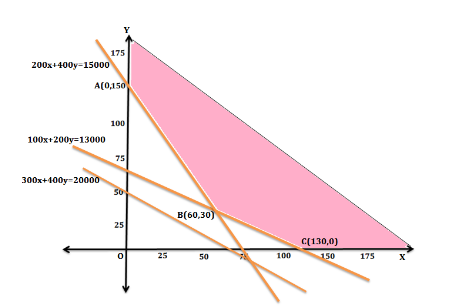
As $x\ge 0,y\ge 0$ solution lies only in the first quadrant. From the graph shaded region is the feasible region.
We get the intersection of the line (1) with the coordinate axes at points (120, 0) and (0, 65).
Similarly, we get intersection of the line (2) with the coordinate axes at points $\left( \dfrac{200}{3},0 \right)=\left( 66.66,0 \right)$ and (0, 50) and the line (3) with the coordinate axes at points (75, 0) and (0, 150).
The common shaded region is a feasible region with corner points A(0, 150), B(60, 30), C(120,0).
Let us find values of the objective function $z=400x+300y$at the corner points A, B and C respectively.
Z (A) = 400(0) + 300(150) = 0 + 45000 =45000
Z (B) = 400(60) + 300(30) = 24000 + 9000 = 33000
Z (C) = 400(120) + 300(0) = 48000 + 0 = 48000
The minimum value of the objective function Z is 33000 at (60, 30).
Hence the value of the function $z=400x+300y$ is minimum when x = 60, y = 30.
Therefore, the correct option is (b).

Note: Let R be the feasible region (convex polygon) for the LPP and let z = ax + by be the objective function. Then the minimum value of z occurs on at least one of the corner points (vertex) of the feasible region.