
An open organ pipe of length L vibrates in a second harmonic mode. The pressure vibration is maximum
(A). At the two ends
(B). At a distance L/4 from either and inside the tube
(C). At the midpoint of the tube
(D). None of these
Answer
516.9k+ views
1 likes
- Hint: In these types of questions remember the basic concepts of harmonic mode and also the formula of the length of an organ pipe .i.e.
Complete step-by-step solution -
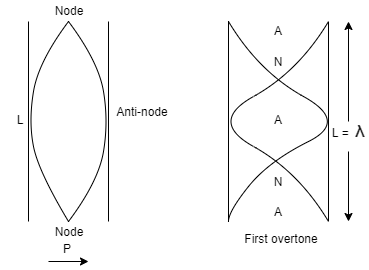
We know that for an open organ pipe, the length L is given as
Where
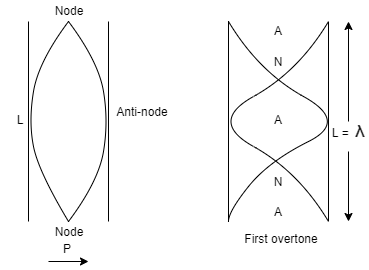
Let substituting n=1 gives for first harmonics and let n=2 gives second harmonics and so on.
Here, an open organ pipe of length L vibrates in second harmonic mode,
Hence the length of the pipe is
Therefore, the length of the pipe at both open ends is equal to the distance between two adjacent antinodes. The nodes are at distance
Because there is no particle displacement at nodes, there is maximal pressure vibration.
Hence, in an open organ pipe, the pressure vibration is maximum at a distance
Note: In the above question a term harmonic frequency is used which can be explained as; every natural frequency produced by an object or instrument has its characteristic vibrational mode or standing wave pattern. Such patterns are produced only at different vibrational frequencies within the object or instrument; such frequencies are known as harmonic frequencies, or merely harmonics. The resulting disturbance to the medium is unpredictable and non-repetitive at any frequency other than a harmonic frequency.
Complete step-by-step solution -

We know that for an open organ pipe, the length L is given as
Where

Let substituting n=1 gives for first harmonics and let n=2 gives second harmonics and so on.
Here, an open organ pipe of length L vibrates in second harmonic mode,
Hence the length of the pipe is
Therefore, the length of the pipe at both open ends is equal to the distance between two adjacent antinodes. The nodes are at distance
Because there is no particle displacement at nodes, there is maximal pressure vibration.
Hence, in an open organ pipe, the pressure vibration is maximum at a distance
Note: In the above question a term harmonic frequency is used which can be explained as; every natural frequency produced by an object or instrument has its characteristic vibrational mode or standing wave pattern. Such patterns are produced only at different vibrational frequencies within the object or instrument; such frequencies are known as harmonic frequencies, or merely harmonics. The resulting disturbance to the medium is unpredictable and non-repetitive at any frequency other than a harmonic frequency.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




