Question

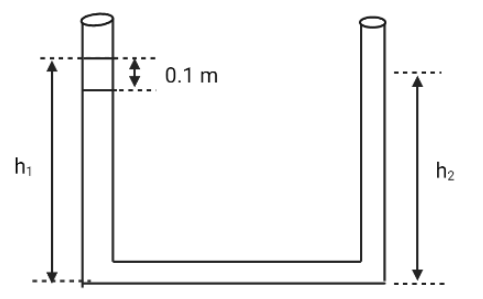
An open-ended U-tube of uniform cross-sectional area contains water (density ${\text{1}}{{\text{0}}^{\text{3}}}{\text{kg}}{{\text{m}}^{\text{3}}}$). Initially the water level stands at ${\text{0}}{\text{.29}}\,{\text{m}}$ from the bottom in each arm. Kerosene oil (a water-immiscible liquid) of density ${\text{800kg}}{{\text{m}}^{\text{3}}}$ is added to the left arm until its length is ${\text{0}}{\text{.1}}\,{\text{m}}$, as shown in the schematic figure below. The ratio ($1/2$) of the heights of the liquid in the two arms is

A. $\dfrac{{15}}{{14}}$
B. $\dfrac{{35}}{{33}}$
C. $\dfrac{7}{6}$
D. $\dfrac{5}{4}$

Answer 1

Hint:The term "density" refers to the amount of mass per unit of volume. An object's average density is equal to its total mass divided by its total volume. An object made of a relatively dense material (such as iron) would have less volume than one made of a less dense substance of equal mass (such as water).

Complete step by step answer:
Temperature and pressure affect the density of a material. For solids and liquids, this variation is usually small, but for gases, it is much greater. When you apply more pressure to an object, it shrinks in volume and thus becomes denser. With a few exceptions, increasing the temperature of a material reduces its density by increasing its volume.

Let us consider ${{\text{h}}_{{\text{1}}\,}}{\text{and}}\,{{\text{h}}_{\text{2}}}$ and add them
${h_1}\, + \,{h_2}\, = \,0.29 \times 2\, + \,0.1$
On further solving we get,
${{\text{h}}_{\text{1}}}\,{\text{ + }}\,{{\text{h}}_{\text{2}}}\,{\text{ = }}\,{\text{0}}{\text{.68}}.........\left( {\text{1}} \right)$
Let ${\rho _k}$denote the density of the kerosene and ${{{\rho }}_{\text{w}}}$ denote the density of water.
${{\text{P}}_{\text{0}}}\,{\text{ + }}\,{{{\rho }}_{\text{k}}}{\text{g}}\left( {{\text{0}}{\text{.1}}} \right)\,{\text{ + }}\,{{{\rho }}_{\text{w}}}{\text{g}}\left( {{{\text{h}}_{\text{1}}}\,{\text{ - }}\,{\text{0}}{\text{.1}}} \right) \\
\Rightarrow {\text{ - }}{{{\rho }}_{\text{w}}}{\text{g}}{{\text{h}}_{\text{2}}}\,{\text{ = }}\,{{\text{P}}_{\text{0}}} \\ $
On substituting and expanding the equations,
\[{{{\rho }}_{\text{k}}}{\text{g}}\left( {{\text{0}}{\text{.1}}} \right)\,{\text{ + }}\,{{{\rho }}_{\text{w}}}{\text{g}}{{\text{h}}_{\text{1}}}\,{\text{ - }}\,{{{\rho }}_{\text{w}}}{\text{g}}\,{{ \times }}\left( {{\text{0}}{\text{.1}}} \right){\text{ = }}\,{{{\rho }}_{\text{w}}}{\text{g}}{{\text{h}}_{\text{2}}} \\ \]
On further substituting,
$800\, \times 10 \times 0.1 + 1000 \times 10 \times {h_1} \\
\Rightarrow \, - 1000\, \times 10 \times 0.1 = 1000 \times 10 \times {h_2} \\ $
On further solving, we get
$10000\left( {{{\text{h}}_{\text{1}}}\,{\text{ - }}\,{{\text{h}}_{\text{2}}}} \right)\, = \,200 \\
\Rightarrow \left( {{h_{\text{1}}}\,{\text{ - }}\,{{\text{h}}_{\text{2}}}} \right)\,\, = \,0.02.................\left( 2 \right) \\ $
Comparing equations $\left( {\text{1}} \right)\,{\text{and}}\,\left( {\text{2}} \right)\,{\text{we}}\,{\text{get,}}$
${{\text{h}}_{\text{1}}}\,{\text{ = }}\,{\text{0}}{\text{.35}}\,\,{\text{;}}\,\,{{\text{h}}_{\text{2}}}\,{\text{ = }}\,{\text{0}}{\text{.33}}$
So, the ratio ($1/2$) of the heights of the liquid in the two arms is,
$\therefore \dfrac{{{{\text{h}}_{\text{1}}}}}{{{{\text{h}}_{\text{2}}}}}\,{\text{ = }}\,\dfrac{{{\text{35}}}}{{{\text{33}}}}$

Hence, the correct option is B.

Note:Heating the bottom of a fluid causes heat to convect from the bottom to the top of most materials due to a reduction in the density of the heated fluid. As a result, it rises in comparison to more dense unheated material.