
An orbiting satellite will escape if
A. Its speed is increased by
B. Its speed in the orbit is made
C. Its KE is doubled
D. It stops moving in the orbit
Answer
491.7k+ views
1 likes
Hint: Firstly, we need to define the orbital velocity and escape velocity of Earth. From these, we can interpret the increase in the speed of the orbital velocity. The kinetic energy is directly proportional to velocity squared. From this, we can know the change in the kinetic energy of the satellite.
Formula used:
Complete answer:
The orbiting satellite moves around the earth with a velocity called Orbital velocity. It is the velocity with which the satellites revolve around the earth, as shown in the figure.
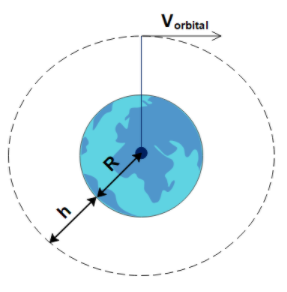
Orbital velocity is mathematically given by
Where,
Keeping this aside, the escape velocity of the Earth is the minimum velocity needed by any object to escape the Earth’s gravitational field.
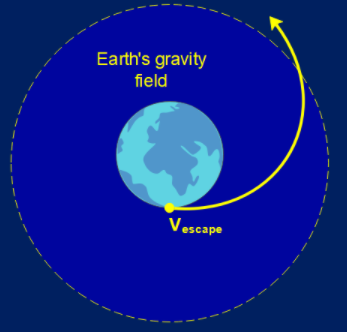
Escape velocity is mathematically given by
An orbiting satellite must reach this velocity to escape Earth’s gravity. Thus, it must increase by
Therefore, the speed increases by 41%.
As the velocity increased by
The kinetic energy for any object can be given by
From this, we have the relation,
Thus, the kinetic energy will be doubled.
Therefore, the correct option is A and C.
Note:
Any satellite will mostly keep rotating in the orbit, like the moon. In case, it stops moving the centripetal velocity will be lost and the satellite will give in to earth’s gravity. Thus, it will crash into Earth’s surface. The escape velocity and orbital velocity can also be written in the terms of acceleration due to gravity.
Formula used:
Complete answer:
The orbiting satellite moves around the earth with a velocity called Orbital velocity. It is the velocity with which the satellites revolve around the earth, as shown in the figure.

Orbital velocity is mathematically given by
Where,
Keeping this aside, the escape velocity of the Earth is the minimum velocity needed by any object to escape the Earth’s gravitational field.

Escape velocity is mathematically given by
An orbiting satellite must reach this velocity to escape Earth’s gravity. Thus, it must increase by
Therefore, the speed increases by 41%.
As the velocity increased by
The kinetic energy for any object can be given by
From this, we have the relation,
Thus, the kinetic energy will be doubled.
Therefore, the correct option is A and C.
Note:
Any satellite will mostly keep rotating in the orbit, like the moon. In case, it stops moving the centripetal velocity will be lost and the satellite will give in to earth’s gravity. Thus, it will crash into Earth’s surface. The escape velocity and orbital velocity can also be written in the terms of acceleration due to gravity.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹31,500 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




