Question

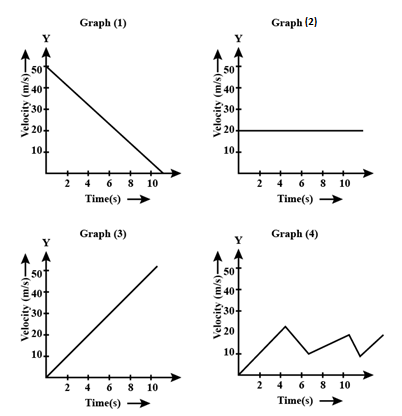
Analyze the graphs given below.
(a). Which graph indicates uniform velocity?
(b). Which graph indicates non uniform acceleration?
(c) .Which graph indicates the motion of freely falling stone?

Answer 1

Hint : We have been given velocity and time for all four cases, and we have to find out the constant velocity graph, non-uniform acceleration graph and free falling graph. Keep in mind that the slope of the velocity-time graph gives us acceleration and that acceleration is a function of time.

Complete step-by-step solution:
Let us look at Graph (2). The velocity \[V\] remains the same even with time \[T\]increasing, which indicates that Graph (2) has constant velocity.
Coming to Graph (3), here let us consider three cases.
When \[{v_1}\]= 10 \[\dfrac{m}{{\sec }}\]and \[{t_1}\]= 2 \[\sec\]
When \[{v_2}\]= 30 \[\dfrac{m}{{\sec }}\] and \[{t_2}\]= 6 \[\sec\]
When \[{v_3}\]= 50 \[\dfrac{m}{{\sec }}\] and \[{t_3}\]= 10 \[\sec\]
Keeping value of \[u\]= 0 as object starts from rest
Using values of 1. To find out acceleration \[{a_1}\]
\[{a_1}\] = \[\dfrac{{{v_1}}}{{{t_1}}}\]
= \[\dfrac{{10}}{2}\] \[\dfrac{m}{{{{\mathop{\rm s}\nolimits} ^2}}}\]
\[{a_1}\]= 5 \[\dfrac{m}{{{{\mathop{\rm s}\nolimits} ^2}}}\] …… (1)
Using values of 2. To find out acceleration \[{a_2}\]
\[{a_2}\] = \[\dfrac{{{v_2}}}{{{t_2}}}\]
= \[\dfrac{{30}}{6}\] \[\dfrac{m}{{{{\mathop{\rm s}\nolimits} ^2}}}\]
\[{a_2}\] = 5 \[\dfrac{m}{{{{\mathop{\rm s}\nolimits} ^2}}}\] ……(2)
Using values of 3. To find out acceleration \[{a_3}\]
\[{a_3}\] = \[\dfrac{{{v_3}}}{{{t_3}}}\]
= \[\dfrac{{50}}{{10}}\]\[\dfrac{m}{{{{\mathop{\rm s}\nolimits} ^2}}}\]
\[{a_3}\] = 5 \[\dfrac{m}{{{{\mathop{\rm s}\nolimits} ^2}}}\] ……(3)
From equation (1), (2) and (3) we get to the result that
\[{a_1}\]= \[{a_2}\] = \[{a_3}\]
Which means this graph shows constant acceleration, which happens during free fall motion.
So , Graph (3) indicates the motion of freely falling stone.
In Graph (4), we can see that the velocities and time at any given point is not constant, because the slope is changing at every point of time. This indicates that the slope isn’t constant, and hence the acceleration is changing at every point of time. This indicates that this graph shows us non-uniform acceleration.
Graph (1) indicates that the object in motion is in uniform – deceleration, because the velocity is decreasing at a constant rate at a constant given time.
So to conclude, we can say that;
Graph (2) gives us graph of constant velocity
Graph (3) gives us motion of a free falling object
Graph (4) gives us a graph of non-uniform acceleration.

Note: In Velocity- time graph, the slope gives us the information needed to find acceleration, which can be found with the equation \[v = u + at\]. Keep in mind that acceleration is a function of time, and the slope of the graph varies with the same.