Question

Angle‌ ‌in‌ ‌a‌ ‌major‌ ‌segment‌ ‌is‌ ‌
(A)‌ ‌An‌ ‌acute‌ ‌angle‌ ‌
(B)‌ ‌An‌ ‌obtuse‌ ‌angle‌ ‌
(C)‌ ‌A‌ ‌right‌ ‌triangle‌ ‌
(D)‌ ‌A‌ ‌reflexive‌ ‌angle‌ ‌

Answer 1

Hint: From the given question we have been asked to find the angle in a major segment. First we have to draw a figure which includes a minor segment $AB$ of a circle and two points $C$ and $D$ in $BA$ and $AB$ respectively. The figure should contain a minor segment and major segment and all angles are needed to be mentioned clearly.

Complete step-by-step solution:
Figure:

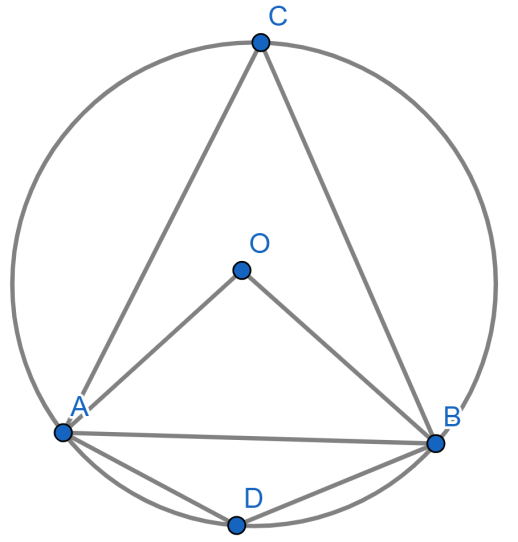
Now considering from the question we have a circle and a major and minor segment in it.
From the figure we can understand that $ACB$ is the major segment in the circle and $ADB$ is the minor segment in the circle. We have to find the angle $ACB$ as it is the major segment.
We know that the angle subtended by an arc of a circle at its centre is twice the angle subtended by it at any point of the alternate segment of the circle. Since $AB$ is the minor arc and angle $ACB$ is the angle formed by it in the alternate segment.
Therefore, from the figure
Therefore, $\text{2}\angle ACB=\angle AOB$
Since $\angle AOB$ is an angle of triangle $AOB$, it will be less than ${{180}^{\circ }}$
Therefore,
$\angle AOB < {{180}^{\circ }}$
 $\text{2}\angle ACB < {{180}^{\circ }}$
$\Rightarrow \angle ACB < {{90}^{\circ }}$
Since the angle $ACB$ is less than ${{90}^{\circ }}$, it is an acute angle.
Therefore, $\angle ACB\text{ }$ is an acute angle.
Therefore, angle in a major segment is an acute angle.
Hence, option A is the correct option.

Note: While answering questions of this type we should surely draw a diagram and observe it carefully and apply the right concepts at the right point. And the basic concept of the circle that we used here is that the angle subtended by an arc of a circle at its centre is twice the angle subtended by it at any point of the alternate segment of the circle. Similarly by using this concept we can prove that the angle in a minor segment is an obtuse angle.