Question

How is the angle of emergence ${{\text{i}}_2}$ related to the angle of incidence ${{\text{i}}_1}$?
$
  {\text{A}}{\text{. }}{{\text{i}}_2} = {{\text{i}}_1} \\
  {\text{B}}{\text{. }}{{\text{i}}_2} < {{\text{i}}_1} \\
  {\text{C}}{\text{. }}{{\text{i}}_2} > {{\text{i}}_1} \\
 $
${\text{D}}{\text{.}}$ Can’t say

Answer 1

Hint: Here, we will proceed by assuming a glass slab placed in air and then, we will pass a beam or ray of light through in order to have the required relation between the angle of incidence and angle of emergence.

Complete Step-by-Step solution:

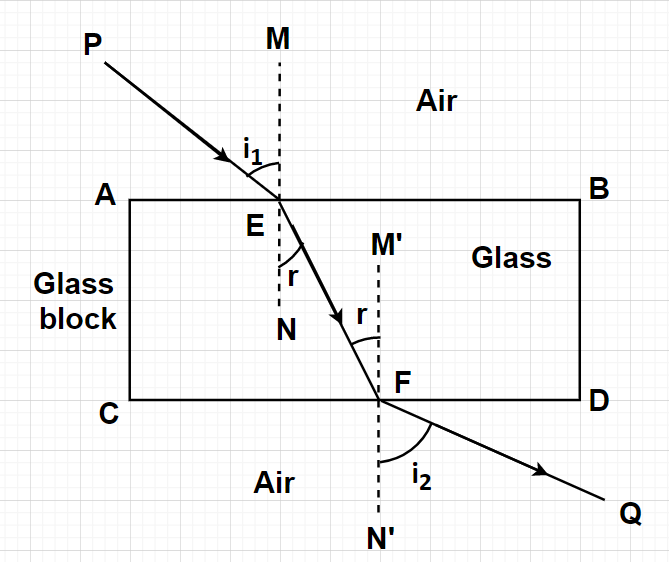
In order to find the relation between the angle of incidence and the angle of emergence, let us consider a glass block with opposite sides being parallel placed in air as shown in figure. One rectangular face ACDB of this glass block is shown in figure.
As we know that whenever a ray of light passes from one medium to another medium having different refractive indices, refraction occurs.
Let us observe a ray of light PE incident on this glass block. Here, at the incident surface (i.e., at point E) the ray of light passing through the air medium to glass will undergo refraction because the medium is changing (and hence the refractive index is also changing). Let the angle of incidence be ${{\text{i}}_1}$ and the angle of refraction at point E be r. Also, let the refractive indices of air and glass be ${\mu _{\text{a}}}$ and ${\mu _{\text{b}}}$ respectively.
According to Snell’s law (or second law of refraction), for a light ray entering from a medium with refractive index ${\mu _{\text{a}}}$ to a medium with refractive index ${\mu _{\text{b}}}$ along with the angle of incidence as ${{\text{i}}_1}$ and the angle of refraction as r, we can write
$
  \dfrac{{\sin {i_1}}}{{\sin r}} = \dfrac{{{\mu _{\text{a}}}}}{{{\mu _{\text{b}}}}} \\
   \Rightarrow \sin r = \dfrac{{{\mu _{\text{b}}}}}{{{\mu _{\text{a}}}}}\left( {\sin {i_1}} \right){\text{ }} \to {\text{(1)}} \\
 $
Now as this refracted ray reaches point F at the interface between two media i.e., glass and air, refraction will again take place. As we can clearly see that the opposite edges of the glass block are parallel i.e., AB is parallel to CD. So, the alternative angles will be equal in measure i.e., the angle of incidence for the second refraction occurring at point F will be equal to r. Let us suppose that the angle of emergence is ${{\text{i}}_2}$.
According to Snell’s law (or second law of refraction), for a light ray entering from a medium with refractive index ${\mu _{\text{b}}}$ (i.e., glass medium) to a medium with refractive index ${\mu _{\text{a}}}$ (i.e., air medium) along with the angle of incidence as ${{\text{i}}_1}$ and the angle of refraction as r, we can write
$
  \dfrac{{\sin r}}{{\sin {i_2}}} = \dfrac{{{\mu _{\text{b}}}}}{{{\mu _{\text{a}}}}} \\
   \Rightarrow \sin r = \dfrac{{{\mu _{\text{b}}}}}{{{\mu _{\text{a}}}}}\left( {\sin {i_2}} \right){\text{ }} \to {\text{(2)}} \\
 $
Clearly, LHS of both the equations (1) and (2) are same so that the RHS of both these equations will also be equal
i.e., $
  \dfrac{{{\mu _{\text{b}}}}}{{{\mu _{\text{a}}}}}\left( {\sin {i_1}} \right) = \dfrac{{{\mu _{\text{b}}}}}{{{\mu _{\text{a}}}}}\left( {\sin {i_2}} \right) \\
   \Rightarrow \sin {i_1} = \sin {i_2} \\
 $
Using the formula $\sin x = \sin y \Rightarrow x = y$ in the above equation, we get
${i_1} = {i_2}$
$ \Rightarrow {i_2} = {i_1}$
The above equation gives the required relation between the angle of emergence ${{\text{i}}_2}$ and the angle of incidence ${{\text{i}}_1}$

Therefore, option A is correct.

Note- The emergence angle is the angle of light coming out of a medium (for example, a parallel sided glass slab). The first medium may be air, and the medium in the middle may be water or a parallel sided glass slab. The beam of light travels through the air at an angle, then hits the glass. When it hits the glass the light refracts or bends, then continues on and emerges again into the air at a new angle.