Question

Angle of maximum deviation is?
(A) ${45^\circ }$
(B) ${\sin ^{ - 1}}\left( {\sqrt 2 \sin {{15}^\circ }} \right)$
(C) ${30^\circ } + {\sin ^{ - 1}}\left( {\sqrt 2 \sin {{15}^\circ }} \right)$
(D) None

Answer 1

Hint: There two ways through which maximum deviation can be achieved one is when the angle is at $90$ degrees. This is also well-known as the grazing incidence and differently is when the emergent light ray after leaving the prism grazes along the surface of the prism.

Formula used:
$\mu = \dfrac{{{v_o}}}{{{v_m}}}$.

Complete step by step answer:
As per the given criteria, Refractive index of the prism, $\mu = \sqrt 2 $
Angle of the prism, $A = {60^\circ }$
The angle of the prism is the angle among two lateral faces of the prism. While a light ray is passed through the prism, it creates an emergent ray and bends at an angle to the direction of incident light rays. This angle is termed as the angle of deviation of the prism.

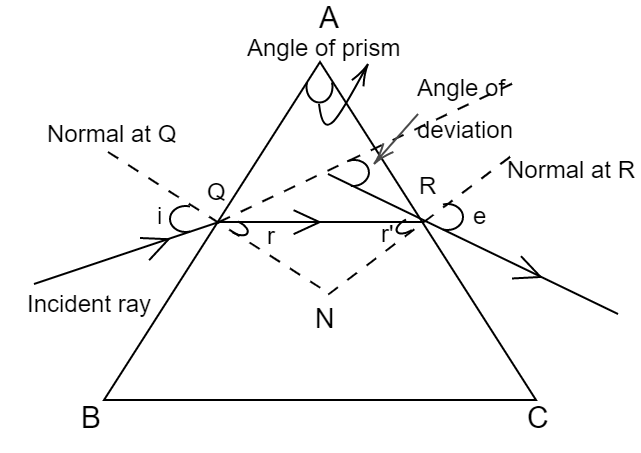
For maximum deviation, emergent ray ought to be parallel to the emergent surface,
i.e., ${r_2} = {\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right)$
Put the value of refractive index in the above equation we get,
$ \Rightarrow {\sin ^{ - 1}}\left( {\dfrac{1}{{\sqrt 2 }}} \right) = {45^\circ }$
Therefore, $A = {r_1} + {r_2}$
Put the value of the $A$ and ${r_2}$ in the above equation we get,
$ \Rightarrow 60 = {r_1} + 45$
$ \Rightarrow {r_1} = 60 - 45 = {15^\circ }$
Since we know that According to Snell’s law,
$\dfrac{{\sin {i_1}}}{{\sin {r_1}}} = \mu $
$ \Rightarrow \sin {i_1} = \mu \times \sin {r_1}$
Substitute all the required values to determine $\angle {i_1}$ in the above equation,
$ \Rightarrow \sin {i_1} = \sqrt 2 \times \sin \left( {15} \right)$
$ \Rightarrow {i_1} = {\sin ^{ - 1}}\left( {\sqrt 2 \times \sin \left( {15} \right)} \right)$
And the deviation produced by the prism is maximum when either angle of incidence or angle of emergence is ${90^\circ }$ . Therefore,
$ \Rightarrow {i_2} = {90^\circ }$
The total deviation will be the sum of the deviation at the two surfaces.
${\delta _{\max }} = \left( {{i_1} - {r_1}} \right) + \left( {{i_2} - {r_2}} \right)$ .
Hence, we can write this equation as,
${\delta _{\max }} = \left( {{i_1} + {i_2} - A} \right)$
where ${i_1}$ is the angle of incidence and ${i_2}$ is the angle of emergence.
Substitute the required values in the above equation to get the answer,
$ \Rightarrow {\delta _{\max }} = {\sin ^{ - 1}}\left( {\sqrt 2 \times \sin \left( {15} \right)} \right) + 90 - 60$
$ \Rightarrow {\delta _{\max }} = {30^\circ } + {\sin ^{ - 1}}\left( {\sqrt 2 \times \sin \left( {15} \right)} \right)$
Hence, the correct answer is option (C).

Note:
The refractive index formula is fixed by applying the angle of incidence and angle of emergent ray in the Snell’s rule. Snell’s law is usually used to describe the relationship between the angle of incidence and refraction between two isotropic media.