Question

What are collisions? Explain the possible types of collisions. Develop the theory of one-dimensional elastic collision.

Answer 1

Hint: Collisions – define it in terms of the laws of conservations they follow. Explain the types of collision based on the conservation laws they followed. Use the law of conservation of momentum and the law of conservation of kinetic energy in an elastic collision to develop the theory of one-dimensional elastic collision.

Complete step-by-step answer:
Collision can be defined as the event in which two moving bodies or one moving body and one at rest collide with each other.
Collision is of two types –
1. Elastic collision
2. Inelastic collision
Elastic collision can be defined as a collision where the total kinetic energy of the system is conserved. In an elastic collision both the total kinetic energy and the total linear momentum of the system remains constant.
In an elastic collision the total kinetic energy of the system will not be conserved. The total kinetic energy before the collision and after the collision will be different.
Consider two bodies, one with mass ${{m}_{1}}$ moving with velocity ${{v}_{1}}$ in the positive x-direction and another body of mass ${{m}_{2}}$at rest.

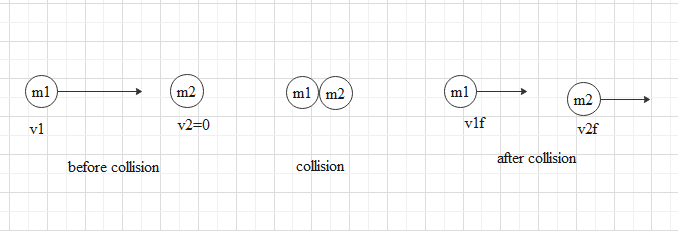
Let, after a time t the two bodies collide. After the collision the velocity of the body with mass ${{m}_{1}}$ becomes ${{v}_{1f}}$ and the velocity of the body of mass ${{m}_{2}}$becomes ${{v}_{2f}}$.
Now, in an elastic collision the linear momentum is conserved,
$\begin{align}
  & {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}={{m}_{1}}{{v}_{1f}}+{{m}_{2}}{{v}_{2f}} \\
 & {{m}_{1}}{{v}_{1}}={{m}_{2}}{{v}_{1f}}+{{m}_{2}}{{v}_{2f}}\to 1 \\
 & {{m}_{1}}({{v}_{1}}-{{v}_{1f}})={{m}_{2}}{{v}_{2f}}\to 2 \\
\end{align}$
Again, total kinetic energy is also conserved,
$\begin{align}
  & \dfrac{1}{2}{{m}_{1}}{{v}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{v}_{2}}^{2}=\dfrac{1}{2}{{m}_{1}}{{v}_{1f}}^{2}+\dfrac{1}{2}{{m}_{2}}{{v}_{2f}}^{2} \\
 & \dfrac{1}{2}{{m}_{1}}{{v}_{1}}^{2}=\dfrac{1}{2}{{m}_{1}}{{v}_{1f}}^{2}+\dfrac{1}{2}{{m}_{2}}{{v}_{2f}}^{2} \\
 & {{m}_{1}}({{v}_{1}}^{2}-{{v}_{1f}}^{2})={{m}_{2}}{{v}_{2f}}^{2} \\
 & {{m}_{1}}({{v}_{1}}-{{v}_{1f}})({{v}_{1}}+{{v}_{1f}})={{m}_{2}}{{v}_{2f}}^{2}\to 3 \\
\end{align}$
Dividing equation 3 by equation 2,
$\begin{align}
  & {{v}_{1}}+{{v}_{1f}}={{v}_{2f}} \\
 & {{v}_{1f}}={{v}_{2f}}-{{v}_{1}}\to 4 \\
\end{align}$
Putting this value on equation 1, we get
\[\begin{align}
  & {{m}_{1}}{{v}_{1}}={{m}_{2}}({{v}_{2f}}-{{v}_{1}})+{{m}_{2}}{{v}_{2f}} \\
 & ({{m}_{1}}+{{m}_{2}}){{v}_{1}}=2{{m}_{2}}{{v}_{2f}} \\
 & {{v}_{2f}}=\dfrac{({{m}_{1}}+{{m}_{2}})}{2{{m}_{2}}}{{v}_{1}} \\
\end{align}\]
Putting this value on equation 4,
$\begin{align}
  & {{v}_{1f}}={{v}_{2f}}-{{v}_{1}} \\
 & {{v}_{1f}}=\dfrac{({{m}_{1}}+{{m}_{2}})}{2{{m}_{2}}}{{v}_{1}}-{{v}_{1}} \\
 & {{v}_{1f}}=\dfrac{({{m}_{1}}+{{m}_{2}}-2{{m}_{2}})}{2{{m}_{2}}}{{v}_{1}} \\
 & {{v}_{1f}}=\dfrac{({{m}_{1}}-{{m}_{2}})}{2{{m}_{2}}}{{v}_{1}} \\
\end{align}$
This way we can find out the final velocities of the two particles from the conservation of momentum and energies.

Note: Most of the collisions in our day to day life are inelastic collisions. We have a special case of inelastic collision which is called the perfectly inelastic collision. In this type of inelastic collision, the two objects will stick together.