What are complementary and supplementary angles?
Answer
Verified360.3k+ views
Hint: Here, we will be proceeding with the help of definition of complementary angles (sum of complementary angles is ${90^0}$) and supplementary angles (sum of supplementary angles is ${180^0}$) and then afterwards observing examples for each case.
Complete step-by-step answer:
The angles whose sum is equal to the measure of ${90^0}$ are called complementary angles. Complementary angles can be easily seen with the help of a diagram.
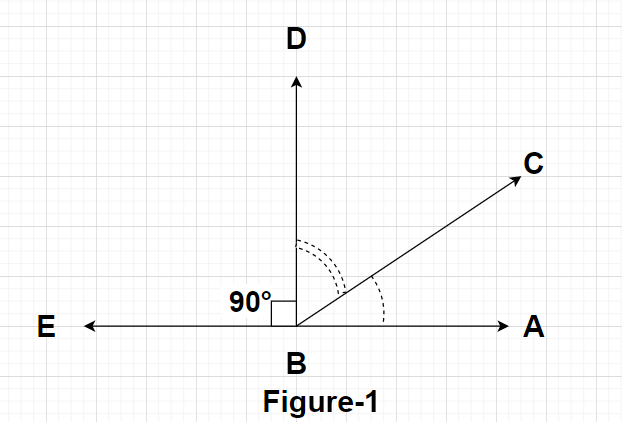
From Figure 1, we can say that $\angle {\text{DBE}} = {90^0}$ and $\angle {\text{ABE}} = {180^0}$
So, $\angle {\text{ABD}} = \angle {\text{ABE}} - \angle {\text{DBE}} = {180^0} - {90^0} = {90^0}$
Clearly, $
\angle {\text{ABD}} = \angle {\text{ABC}} + \angle {\text{CBD}} \\
\Rightarrow {90^0} = \angle {\text{ABC}} + \angle {\text{CBD}} \\
\Rightarrow \angle {\text{ABC}} + \angle {\text{CBD}} = {90^0}{\text{ }} \to {\text{(1)}} \\
$
From equation (1), we can say that since the sum of angles $\angle {\text{ABC}}$ and $\angle {\text{CBD}}$ is equal to ${90^0}$ so these two angles are known as complementary angles.
The angles whose sum is equal to the measure of ${180^0}$ are called supplementary angles. Supplementary angles can be easily seen with the help of a diagram.
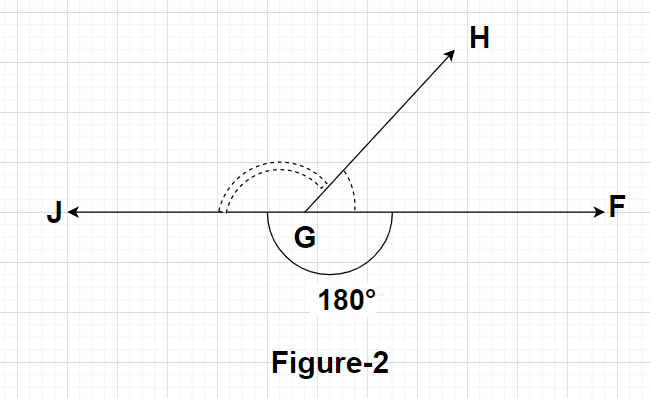
From Figure 2, we can say that $\angle {\text{FGJ}} = {180^0}$
So, $
\angle {\text{FGJ}} = \angle {\text{FGH}} + \angle {\text{HGJ}} \\
\Rightarrow {180^0} = \angle {\text{FGH}} + \angle {\text{HGJ}} \\
\Rightarrow \angle {\text{FGH}} + \angle {\text{HGJ}} = {180^0}{\text{ }} \to {\text{(2)}} \\
$
From equation (2), we can say that since the sum of angles $\angle {\text{FGH}}$ and $\angle {\text{HGJ}}$ is equal to ${180^0}$ so these two angles are known as supplementary angles.
Note: If we consider all the interior angles of any triangle, then we can say that all these interior angles of any triangle constitutes supplementary angles because the sum of all the interior angles of a triangle gives a measure of ${180^0}$ (according to the property of a triangle).
Complete step-by-step answer:
The angles whose sum is equal to the measure of ${90^0}$ are called complementary angles. Complementary angles can be easily seen with the help of a diagram.
From Figure 1, we can say that $\angle {\text{DBE}} = {90^0}$ and $\angle {\text{ABE}} = {180^0}$
So, $\angle {\text{ABD}} = \angle {\text{ABE}} - \angle {\text{DBE}} = {180^0} - {90^0} = {90^0}$
Clearly, $
\angle {\text{ABD}} = \angle {\text{ABC}} + \angle {\text{CBD}} \\
\Rightarrow {90^0} = \angle {\text{ABC}} + \angle {\text{CBD}} \\
\Rightarrow \angle {\text{ABC}} + \angle {\text{CBD}} = {90^0}{\text{ }} \to {\text{(1)}} \\
$
From equation (1), we can say that since the sum of angles $\angle {\text{ABC}}$ and $\angle {\text{CBD}}$ is equal to ${90^0}$ so these two angles are known as complementary angles.
The angles whose sum is equal to the measure of ${180^0}$ are called supplementary angles. Supplementary angles can be easily seen with the help of a diagram.
From Figure 2, we can say that $\angle {\text{FGJ}} = {180^0}$
So, $
\angle {\text{FGJ}} = \angle {\text{FGH}} + \angle {\text{HGJ}} \\
\Rightarrow {180^0} = \angle {\text{FGH}} + \angle {\text{HGJ}} \\
\Rightarrow \angle {\text{FGH}} + \angle {\text{HGJ}} = {180^0}{\text{ }} \to {\text{(2)}} \\
$
From equation (2), we can say that since the sum of angles $\angle {\text{FGH}}$ and $\angle {\text{HGJ}}$ is equal to ${180^0}$ so these two angles are known as supplementary angles.
Note: If we consider all the interior angles of any triangle, then we can say that all these interior angles of any triangle constitutes supplementary angles because the sum of all the interior angles of a triangle gives a measure of ${180^0}$ (according to the property of a triangle).
Last updated date: 18th Sep 2023
•
Total views: 360.3k
•
Views today: 7.60k
