
What are forced vibrations and resonance? Show that only odd harmonics are present in an air column vibrating in a pipe closed at one end. A stretched wire emits a fundamental note of frequency
Answer
475.8k+ views
Hint: To solve this question, we need to use the relation between the frequency and the length of a stretched string from
Formula used: The formulae used to solve this question are given by
Complete step by step answer
When a system oscillates in a medium, there is some amount of damping present in the system, which eventually finishes out the oscillation. This damping is due to the viscous force of water, drag force of air etc. which always acts opposite to the relative motion of the system. So, to maintain the oscillations, we apply external periodic force. Then the system oscillates with the frequency equal to the frequency of the force, as the natural oscillations die out due to damping. These oscillations or vibrations are known as forced vibrations.
The amplitude in the forced vibrations is given by
We can clearly observe that when the driving frequency is very much close to the natural frequency, then amplitude becomes maximum, which is given by
This phenomenon of maximising the amplitude, by setting the driving frequency close to the natural frequency is termed as resonance.
Let us consider an air column of length
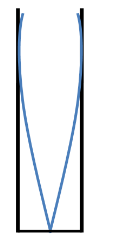
We know that the distance between a node and an antinode is equal to
We know that the frequency is given by
So from (1) the fundamental frequency is
Now, let us consider the air column for the first overtone.
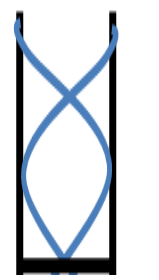
For this case, we have
So the first overtone frequency becomes
From (2)
Similarly, for the
So we see from the above expression that the overtone frequencies are the odd multiples of the fundamental frequency. So, only odd harmonics are present in an air column vibrating in a pipe closed at one end.
We know that the velocity of wave in a stretched string is given by
The fundamental frequency of the wave in a stretched string is given by
According to the question, the frequency is given as
Now, when the length is reduced by
Dividing (4) by (3) we get
On solving the above equation, we get the original length of the wire as
Hence, the original length of the wire is equal to
Note
There will be no change in the velocity of the wave in the stretched wire given in the question. The tension is already given to be constant. And the mass per unit length will also not change, as it is the property of material of the wire.
Formula used: The formulae used to solve this question are given by
Complete step by step answer
When a system oscillates in a medium, there is some amount of damping present in the system, which eventually finishes out the oscillation. This damping is due to the viscous force of water, drag force of air etc. which always acts opposite to the relative motion of the system. So, to maintain the oscillations, we apply external periodic force. Then the system oscillates with the frequency equal to the frequency of the force, as the natural oscillations die out due to damping. These oscillations or vibrations are known as forced vibrations.
The amplitude in the forced vibrations is given by
We can clearly observe that when the driving frequency is very much close to the natural frequency, then amplitude becomes maximum, which is given by
This phenomenon of maximising the amplitude, by setting the driving frequency close to the natural frequency is termed as resonance.
Let us consider an air column of length

We know that the distance between a node and an antinode is equal to
We know that the frequency is given by
So from (1) the fundamental frequency is
Now, let us consider the air column for the first overtone.

For this case, we have
So the first overtone frequency becomes
From (2)
Similarly, for the
So we see from the above expression that the overtone frequencies are the odd multiples of the fundamental frequency. So, only odd harmonics are present in an air column vibrating in a pipe closed at one end.
We know that the velocity of wave in a stretched string is given by
The fundamental frequency of the wave in a stretched string is given by
According to the question, the frequency is given as
Now, when the length is reduced by
Dividing (4) by (3) we get
On solving the above equation, we get the original length of the wire as
Hence, the original length of the wire is equal to
Note
There will be no change in the velocity of the wave in the stretched wire given in the question. The tension is already given to be constant. And the mass per unit length will also not change, as it is the property of material of the wire.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




