Question

What are the distinct intersecting lines?

Answer 1

Hint: We will use the concept of intersecting lines in which any two distinct lines cut each other in any dimensional plane.

Complete step-by-step answer:

The diagram of the intersecting lines is given below.

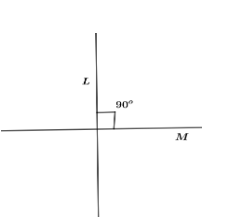
We will consider two different lines namely L and M. These two lines are chosen here in a way that there is only one point in common. As it raises a question here why this type of the two lines are considered here. So, to clear the confusion we will take two parallel lines. If the lines L and M are parallel then that means that either no point is in common between them or they are coinciding resulting into two parallel lines in which the lines L and M have infinite many points in common. So, now we will consider whether these points are intersecting or not. For this we will first consider the set of L and M as two parallel lines as shown below.

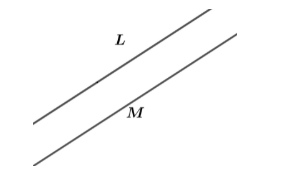
Clearly these points are parallel so after covering infinite distance in any dimensional plane they will never intersect. And since we are supposed to define two distinct intersecting lines so clearly this case does not fit here. Now we will consider the case in which the lines L and M are coinciding. This means that the lines L and M have infinitely many points in common. Now if we look at the coinciding lines we come to know that the one line is looking as if the inverse mirror image of the other line. Or the line L and M are just exactly the same to each other. So, there is no chance that we are taking different lines as these are the same lines that we are considering here.

Now, we have come to know that the lines are not parallel and the lines L and M cannot be coinciding as well. So we are left with the case in which the two different lines L and M are intersecting for sure at only one point. Now this type of intersection can happen only if the lines intersect diagonally or if the lines are perpendicular to each other. Here we will first consider perpendicular lines. So now we have that the lines L and M are perpendicular to each other at ${{90}^{\circ }}$. Clearly, these are distinct and intersecting so this type of the set is selected as distinct intersecting lines. Now we will consider the set of intersecting lines at only one point in which the degree is not ${{90}^{\circ }}$. Since here also we are taking two different lines and they are also intersecting so this set of lines is also selected.
Hence, there are two types of intersecting lines in which the lines are either perpendicular or diagonally intersecting.

Note: If the coinciding lines are considered here then it will result in the wrong answer as we are supposed to take two different lines. And coinciding lines are just that same. Similarly parallel lines do not have any common point.