Question

What are the rotational symmetric orders of the following: Parallelogram, Rectangle, Square, Rhombus, Kite and Trapezium? (Trapezium, not Trapezoid)

Answer 1

Hint: We need to find the rotational symmetric orders of the given figures. We start to solve the question by observing the rotations required for the given figures to look alike. Then, we write the orders of symmetry for the figures to get the required result.

Complete step by step solution:
We are given geometric figures and need to find the rotational symmetric orders for the figures. We will be solving the given question by observing the rotations required for a figure to turn into itself.

Rotational symmetry, also known as radial symmetry, is a property of a shape to look alike after some rotation about its own axis by a partial turn.
It is the smallest angle a geometric figure can be rotated to coincide or look alike like its original figure.
The order of the rotational symmetry of the shape is the number of times it can be rotated around a full circle or 360 to look like its original figure.
According to our question,
The figure of a Parallelogram can be represented as follows,

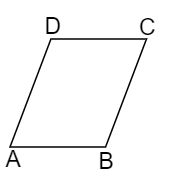
The figure coincides with the original figure after a rotation on 180.
$\therefore $ The order of rotational symmetry of the parallelogram is 2.
The figure of a Rectangle can be represented as follows,

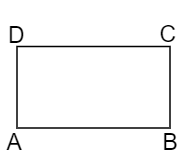
The figure coincides with the original figure after a rotation on 180.
$\therefore $ The order of rotational symmetry of the rectangle is 2.
The figure of a Square can be represented as follows,

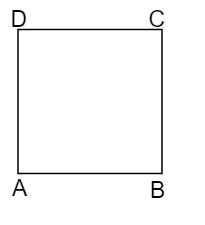
The figure coincides with the original figure after a rotation on 90.
$\therefore $ The order of rotational symmetry of the square is 4.
The figure of a Rhombus can be represented as follows,

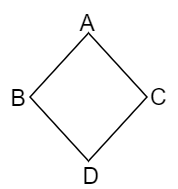
The figure coincides with the original figure after a rotation on 180.
$\therefore $ The order of rotational symmetry of the rhombus is 2.
The figure of a Kite can be represented as follows,

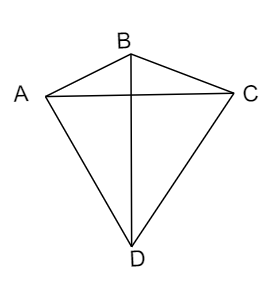
The figure coincides with the original figure after a rotation on 360.
$\therefore $ The order of rotational symmetry of the kite is 1.
The figure of a Trapezium can be represented as follows,

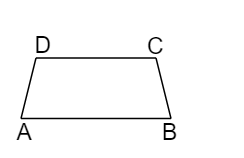
The figure coincides with the original figure after a rotation on 360.
$\therefore $ The order of rotational symmetry of the trapezium is 1.

Note: The order of symmetric rotation is the angle 360 divided by the angle of rotation of the geometric figure. We should know the shapes of geometric figures to find the rotational symmetric orders of the figures.