Question

What are x-coordinate and y-coordinate called?

Answer 1

Hint: We will describe what we understand by knowing the x-coordinate and the y-coordinate. We will look at the x-axis and the y-axis, and the plane formed by these two axes. We will study the four quadrants formed by these axes by seeing the change in the x-coordinate and the y-coordinate in every quadrant.

Complete step by step answer:
The x-coordinate gives us the distance of a point from the vertical axis, that is, the y-axis. The x-coordinate is also called abscissa. The y-coordinate tells us the distance of a point from the horizontal axis, that is, the x-axis. The y-coordinate is also called the ordinate. The two axes, x-axis and y-axis form the xy-plane. We can see it in the figure below,
  

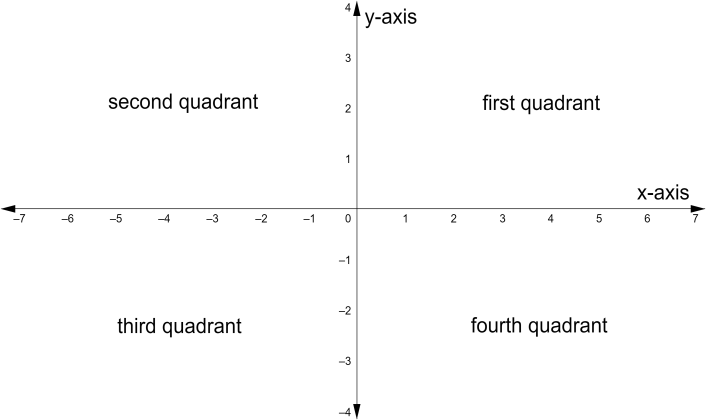
While denoting the location of a point on the xy-plane, we use the following format: $\left( x,y \right)$, here $x$ is the x-coordinate and $y$ is the y-coordinate.
In the figure above, we can see that the xy-plane is divided into four quadrants. The first quadrant consists of all positive x-coordinates and all positive y-coordinates. The second quadrant has negative x-coordinates and positive y-coordinates. In the third quadrant all the x-coordinates as well as all the y-coordinates are negative. The fourth quadrant has positive x-coordinates and negative y-coordinates.

Note: The y-axis that lies above the x-axis is called as the positive y-axis and the y-axis that lies below the x-axis is called as the negative axis. This is intuitive, since the positive y-axis has all positive y-coordinates and the negative y-axis has all the negative y-coordinates. Similarly, The x-axis to the right side of the y-axis is called as the positive x-axis and to the left of the y-axis is called as the negative x-axis. For convenience, we can denote the positive axes as x-axis and y-axis and the negative axes by $\text{x }\!\!'\!\!\text{ }$-axis and $\text{y }\!\!'\!\!\text{ }$-axis.