Question

What is the area of a regular hexagon circumscribed inside a circle with a radius of $1?$

Answer 1

Hint: We will cut the given regular hexagon into six pieces of equilateral triangles. Then we will use the Heron’s formula to find the area of one triangle since each triangle is similar to each other. And then we can multiply this area with six to get the total area of the regular hexagon.

Complete step-by-step answer:
Let us consider the given problem. We are asked to find the area of a regular hexagon circumscribed inside a circle of radius $1$ unit.

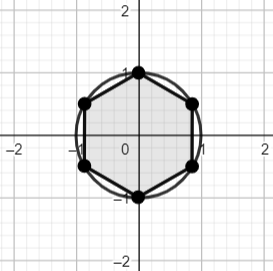
So, that means, each side of the hexagon is equal to $1$ unit.
Now, let us divide the hexagon into six equilateral triangles.
Now, we will consider only one of the six equilateral triangles.
Since it is an equilateral triangle, all sides are equal to $1$ unit.
Therefore, the perimeter of the triangle is equal to $2s=3.$
We will get, the half of the perimeter $s=\dfrac{3}{2}.$
Now, we will use the Heron’s formula to find the area of the triangle.
We will get $area=\sqrt{\dfrac{3}{2}\left( \dfrac{3}{2}-1 \right)\left( \dfrac{3}{2}-1 \right)\left( \dfrac{3}{2}-1 \right)}.$
This will give us $area=\sqrt{\dfrac{3}{2}\dfrac{1}{2}\dfrac{1}{2}\dfrac{1}{2}}=\sqrt{\dfrac{3}{16}}.$
And now we will get, the area of the triangle is equal to $area=\dfrac{\sqrt{3}}{4}.$
Hence the total area of the regular hexagon is equal to $area=6\dfrac{\sqrt{3}}{4}=\dfrac{3\sqrt{3}}{2}$ square units.

Note: We know that the Heron’s formula to find the area of a triangle with sides $a,b$ and $c$ and perimeter $2s$ is given by $area=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}.$ We can also divide the equilateral triangle into two right triangle, then use Pythagoras theorem to find the height and then we will use the formula $area=\dfrac{1}{2}bh$ to find the area then multiplying it with two will give us the area of the equilateral triangle. We can multiply it with six to get the total area of the given hexagon.