
Why is the area under the Velocity time graph the distance?
Answer
417.3k+ views
Hint: The displacement of moving objects with constant velocity is equal to the product of the object velocity and the amount of time the object is in motion.
We need a velocity-time graph when the object’s velocity gets changed.
The area under the velocity-time graph is known as displacement.
Complete step-by-step solution:
Let us draw the distance-time graph of the body from the position
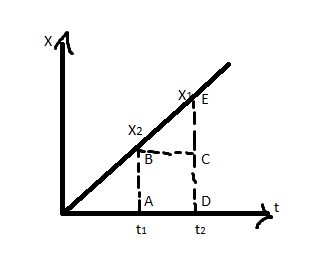
In the above diagram, the area under the curve is equal to the area of the triangle
Then this equation becomes,
We have to solve the above equation then it becomes,
After simplification the equations are,
In the above equations When we consider the unit of term on the right-hand side, it gives
From this area under the distance-time graph gives nothing, Now draw the graph of the velocity of the body concerning the time
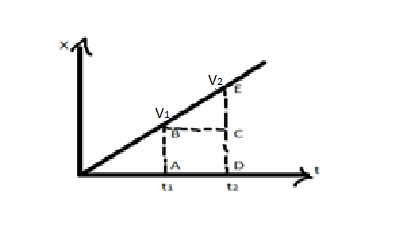
The expression for the area under the curve is as follows,
The equation becomes,
after solving the above equation,
Hence it becomes,
In the above equation, the right-hand side determines the unit we get,
Here, the area under the curve of the velocity-time graph gives the distance covered by the object
Note:The velocity of the body is determined by the gradient curve in the distance-time graph.
The acceleration of the body is determined by the gradient curve in the velocity-time graph.
By integrating the curve we can calculate the area under the curve.
We need a velocity-time graph when the object’s velocity gets changed.
The area under the velocity-time graph is known as displacement.
Complete step-by-step solution:
Let us draw the distance-time graph of the body from the position

In the above diagram, the area under the curve is equal to the area of the triangle
Then this equation becomes,
We have to solve the above equation then it becomes,
After simplification the equations are,
In the above equations When we consider the unit of term on the right-hand side, it gives
From this area under the distance-time graph gives nothing, Now draw the graph of the velocity of the body concerning the time

The expression for the area under the curve is as follows,
The equation becomes,
after solving the above equation,
Hence it becomes,
In the above equation, the right-hand side determines the unit we get,
Here, the area under the curve of the velocity-time graph gives the distance covered by the object
Note:The velocity of the body is determined by the gradient curve in the distance-time graph.
The acceleration of the body is determined by the gradient curve in the velocity-time graph.
By integrating the curve we can calculate the area under the curve.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




