Question

As we observed from the top of a 75 m lighthouse from the sea level, the angle of depression of 2 ships \[{{30}^{\circ }}\] and \[{{45}^{\circ }}\]. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between two ships.

Answer 1

Hint: Draw a rough figure of the lighthouse and 2 boats and mark the angle of depression. Consider the triangle where \[{{30}^{\circ }}\] and \[{{45}^{\circ }}\] are formed. Use Pythagoras theorem to find the distance between the 2 ships.

Complete step-by-step answer:
Given is the height of the lighthouse = 75 m.

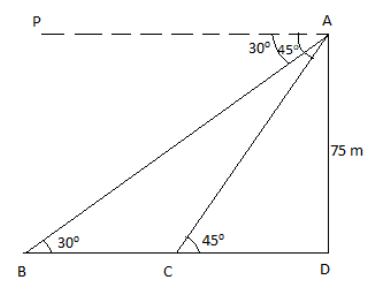
Hence from the figure, we can say that, AD = 75 m
Let the angle of depression of first ship be \[{{45}^{\circ }},\angle PAC={{45}^{\circ }}.\]
The angle of depression of second ship will be \[{{30}^{\circ }},\angle PAB={{30}^{\circ }}.\]
We need to find the distance between the 2 ships, i.e. we need to find the length of BC.
From the figure, we can understand that lines PA and BD are parallel, i.e. \[PA||BD\].
Thus AB and AC are transversals.
We can say that,
\[\begin{align}
  & \angle ABD=\angle PAB={{30}^{\circ }} \\
 & \angle ACD=\angle PAC={{45}^{\circ }} \\
\end{align}\]
where both these angles are alternate angles as \[PA||BD\].
\[\angle ABD={{30}^{\circ }}\] and \[\angle ACD={{45}^{\circ }}\].
The lighthouse is perpendicular to the ground, i.e. \[AD\bot BD\].
\[\therefore \angle ADB={{90}^{\circ }}\].
From the figure, let us consider \[\Delta ACD.\]
\[\tan {{45}^{\circ }}=\dfrac{Side\text{ }opposite\text{ }to\text{ }angle\text{ }C}{Side\text{ }adjacent\text{ }to\text{ }angle\text{ }C}=\dfrac{AD}{CD}\].
We know AD = 75 m, let’s find CD and by trigonometric table \[\tan {{45}^{\circ }}=1\].
\[\begin{align}
  & \tan {{45}^{\circ }}=\dfrac{75}{CD} \\
 & \therefore CD=\dfrac{75}{\tan 45}=\dfrac{75}{1} \\
 & \therefore CD=75cm. \\
\end{align}\]
Now let us consider \[\Delta ABD\].
\[\tan {{30}^{\circ }}=\dfrac{Side\text{ }opposite\text{ }to\text{ }angle\text{ }B}{Side\text{ }adjacent\text{ }to\text{ }angle\text{ }B}=\dfrac{AD}{BD}=\dfrac{AD}{BC+CD}.\]
We know AD = 75 m, CD = 75 cm, and from trigonometric table,
\[\begin{align}
  & \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}} \\
 & \dfrac{1}{\sqrt{3}}=\dfrac{75}{BC+75} \\
\end{align}\]
Cross multiply and find the value of BC.
\[\begin{align}
  & BC+75=75\sqrt{3} \\
 & BC=75\sqrt{3}-75 \\
 & BC=75\left( \sqrt{3}-1 \right)m. \\
\end{align}\]
Thus we got the distance between 2 ships as \[75\left( \sqrt{3}-1 \right)m\].
Hence, distance between 2 ships \[=75\left( \sqrt{3}-1 \right)m.\]

Note:
We have been given the angle of depression which is the angle from the top of the lighthouse to the bottom 2 ships. But as the lines formed are parallel they become alternate angles. So the elevation from the 2 boats to the top of the lighthouse will become \[{{45}^{\circ }}\] and \[{{30}^{\circ }}\].