Question

Assertion: Time taken by a particle in SHM to move from $x = A$ to $x=\dfrac{\sqrt{3}A}{2}$ is same as the time taken by the particle to move from $x = \dfrac{\sqrt{3}A}{2}$ to $x =\dfrac{A}{2}$.
Reason: Corresponding angles in the reference circle are the same in the given time interval.
A. If both Assertion and Reason are true and the Reason is the correct explanation of the Assertion.
B. If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
C. If Assertion is true, but the Reason is false.
D. If Assertion is false but the Reason is true.

Answer 1

Hint: SHM stands for Simple Harmonic Motion .It is a type of oscillating motion. An object oscillates sinusoidally about an equilibrium point during a SHM. Here, we need to find the time interval for both intervals using the standard equation of SHM. We also need to check the truth value of the reason statement and check if it is a good explanation for the assertion statement.

Formula used:
The motion of SHM can be described as:
$x={{x}_{0}}\cos \left( \omega t+\phi \right)$
where, ${{x}_{0}}$ and $\phi $ are constants, and $\omega $ is the angular frequency of the oscillations.

Complete step by step answer:
Let us consider the assertion statement. Given that, at the instant $t=0$ , the particle will be at point $A$ which is $x=A$ with phase equal to zero.
At the instant say $t=t_1$ , the particle will be at point $B$ which is $x=\dfrac{\sqrt{3}A}{2}$
At the instant say $t=t_2$ , the particle will be at point $C$ which is $x=\dfrac{A}{2}$
Now we know the displacement equation is given by
$x={{x}_{0}}\cos \left( \omega t \right)$ as the initial phase $\phi =0$
Now, let us substitute the conditions at time $t=0$
$A={{x}_{0}}\cos \left( \omega (0) \right)$
$\therefore {{x}_{0}}=A$
Substituting the obtained value in the standard equation,
$x=A\cos \left( \omega t \right)$
Now, when the particle is at point $B$ that is $x=\dfrac{\sqrt{3}A}{2}$ , the equation of SHM can be written as
$\dfrac{\sqrt{3}A}{2}=A\cos \left( \omega {{t}_{1}} \right)$
$\therefore \cos \left( \omega {{t}_{1}} \right)=\dfrac{\sqrt{3}}{2}\Rightarrow \omega {{t}_{1}}=\dfrac{\pi }{6}$
Now, we know that angular frequency can be written as $\omega =\dfrac{2\pi }{T}$
$\left( \dfrac{2\pi }{T} \right){{t}_{1}}=\dfrac{\pi }{6} \\
\Rightarrow \dfrac{\pi (T)}{6(2\pi )}=\dfrac{T}{12}$…… $(1)$
Now, when the particle is at point $C$ that is $x=\dfrac{A}{2}$ , the equation of SHM can be written as
$\dfrac{A}{2}=A\cos \left( \omega {{t}_{2}} \right) \\$
$\therefore \cos \left( \omega {{t}_{2}} \right)=\dfrac{1}{2} \\
\Rightarrow \omega {{t}_{2}}=\dfrac{\pi }{3}$
Now, we know that angular frequency can be written as
$\omega =\dfrac{2\pi }{T}$
$\Rightarrow \left( \dfrac{2\pi }{T} \right){{t}_{2}}=\dfrac{\pi }{3} \\
\Rightarrow \dfrac{\pi (T)}{3(2\pi )}=\dfrac{T}{6}$…… $(2)$
Now, the time taken by the particle to reach from $A$ to $B$ is
$T={{t}_{1}}-t=\dfrac{T}{12}-0=\dfrac{T}{12}$
Now, the time taken by the particle to reach from $B$ to $C$ is
$T={{t}_{2}}-{{t}_{1}}=\dfrac{T}{6}-\dfrac{T}{12}=\dfrac{T}{12}$
Hence, the time taken in both intervals is the same. Hence, the assertion statement is correct.

Now, let us consider the reason statement.

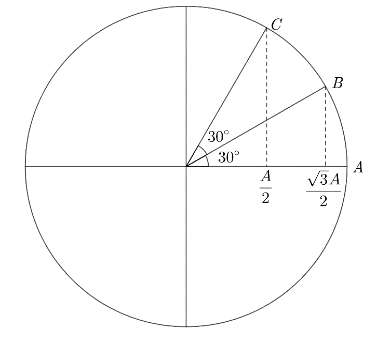
The reference circle in SHM is a circle with radius equal to the amplitude as shown above
We know that the time interval for both the conditions given here is the same. We can say from the figure that when we plot the given conditions on the reference circle, the corresponding angle rotation is also equal. Hence, the reason statement is correct and a correct explanation for the assertion statement.

Hence, the correct option is A.

Note: SHM or Simple Harmonic Motion uses a lot of new concepts and words that you people are familiar with but the basic concepts are the same so if you get stuck at any point of time keep in mind the things you studied in lower classes.