Question

Asymptotes of the function xy = 1 is/are
A. $x=\infty$
B. x = 0
C. y = 0
D. $y=\infty$

Answer 1

Hint: We need to find the asymptotes of the function xy = 1. We start to solve the given question by plotting the graph for the function xy = 1. Then, we find the asymptotes of the function from the graph to get the desired result.

Complete step by step answer:
We are given a function xy = 1 and are asked to find the asymptotes of the given function. We will be solving the given question by plotting the graph for the function xy = 1 and then finding out the asymptotes of the function.
An asymptote is a straight line that approaches a given curve but does meet the curve at any infinite distance. It is the straight line that a curve approaches as the curve heads to infinity.
According to our question,
We are asked to find out the asymptotes of the function xy = 1.
$\Rightarrow xy=1$
The above function can also be written as follows,
$\Rightarrow y=\dfrac{1}{x}$
Applying the limits on the right-hand side, we get,
$\Rightarrow y=\displaystyle \lim_{x \to 0}\dfrac{1}{x}$
From the above, we can see that the curve xy =1 approaches line y = 0 as the curve leads to infinity. So, the line y = 0 is the asymptote of the curve xy = 1.
Now,
$\Rightarrow xy=1$
The above function can also be written as follows,
$\Rightarrow x=\dfrac{1}{y}$
Applying the limits on the right-hand side, we get,
$\Rightarrow x=\displaystyle \lim_{x \to 0}\dfrac{1}{y}$
From the above, we can see that the curve xy =1 approaches line x = 0 as the curve leads to infinity. So, the line x = 0 is the asymptote of the curve xy = 1.
The graph of the curve is given as follows,

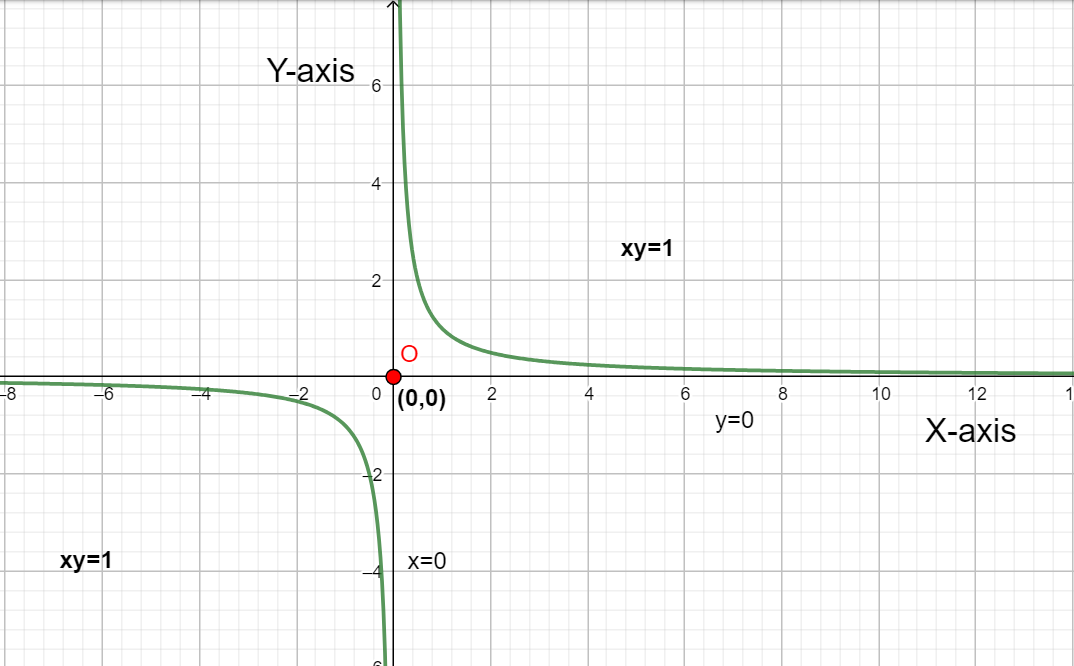
$\therefore$ The Asymptotes of the function xy = 1 are x = 0 and y = 0.
Hence, options B and C hold the correct answer for the given question.

Note: There are three types of asymptotes namely, horizontal, vertical, and oblique asymptotes. In the given question the straight line x = 0 is a vertical asymptote and the straight line y = 0 is a horizontal asymptote of the function xy = 1.