Question

At 3:40, the hour and minute hand are inclined at \[\]
A.$\dfrac{2{{\pi }^{c}}}{3}$\[\]
B.$\dfrac{7{{\pi }^{c}}}{12}$\[\]
C.$\dfrac{13{{\pi }^{c}}}{18}$\[\]
D.$\dfrac{10{{\pi }^{c}}}{18}$\[\]

Answer 1

Hint: We find ${{\theta }_{H}}$ , the angle hour hand makes when it moves from 12o’clock to 3:40 and ${{\theta }_{M}}$ be the angle minute hand makes when it moves from 12o’clock to 3:40 using the fact that both hour hand and minute hand make ${{30}^{\circ }}$ when they move from one number to another in the clock. The required angle in degree is $\theta ={{\theta }_{M}}-{{\theta }_{H}}$ which we convert to radian as $\dfrac{{{\theta }^{\circ }}}{{{180}^{\circ }}}\times {{\pi }^{c}}$.\[\]

Complete step by step answer:
We know that in a watch the 12 numbers from 1 to 12 to represent the measurement of time. The hour hand is the shortest hand in the watch which moves from one number to another to represent the passing one hour. The minute hand is the longer hand which moves from one number to another to represent the passing of 5 minutes. \[\]
When either of hour hand or minute hand move from 12 and then circle back to 12 they subtend a complete angle of measure${{360}^{\circ }}$. So the measure of angle when hour hand or minute hand when they move from one number to other is $\dfrac{360}{12}={{30}^{\circ }}$. \[\]
So an hour hand makes ${{30}^{\circ }}$ in 1 hour and a minute hand makes ${{30}^{\circ }}$ in every 5 minutes. We are asked to find the angle of inclination in between the hour and minute hand at 3:40. Let ${{\theta }_{H}}$ be the angle hour hand makes when it moves from 12o’clock to 3:40 and let ${{\theta }_{M}}$ be the angle minute hand makes when it moves from 12o’clock to 3:40. the angle between hour and hand minute hand is $\theta ={{\theta }_{M}}-{{\theta }_{H}}$.\[\]

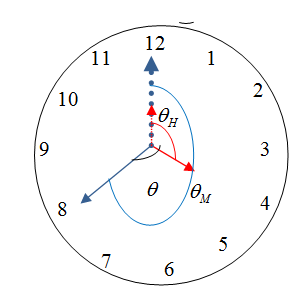
We see that when the hour hand moves from 12 to 3 it passes three numbers and points somewhere in between 3 to 4 to show the position for an additional 40 minutes. We know that 60 minute is 1 hour. So 40 minute is $40\times \dfrac{1}{60}=\dfrac{2}{3}$ hours. So the hour hand has passed from 12 o’clock to 3:40 it passes $3\dfrac{2}{3}=\dfrac{11}{3}$ hours. So we have
\[{{\theta }_{H}}=\dfrac{11}{3}\times {{30}^{\circ }}={{110}^{\circ }}\]
We see that the minute hand moves from 12 o’clock to 8 to show $8\times 5=40$ minutes it passes 8 numbers. So we have,
\[{{\theta }_{M}}=8\times {{30}^{\circ }}={{240}^{\circ }}\]
So we have the angle of inclination is
\[\theta ={{\theta }_{H}}-{{\theta }_{M}}={{240}^{\circ }}-{{110}^{\circ }}={{130}^{\circ }}\]
Let us convert the above measurement in to radian and have,
\[\theta =\dfrac{{{130}^{\circ }}}{{{180}^{\circ }}}\times {{\pi }^{c}}=\dfrac{13{{\pi }^{c}}}{18}\]

So, the correct answer is “Option C”.

Note: We note that we have frequently used the unitary method with direct variation here where we first the value of a single unit by dividing then finding the necessary value by multiplying. We can directly find the required angle as by the formula $\Delta \theta =\left| {{\theta }_{h}}-{{\theta }_{m}} \right|$ where ${{\theta }_{h}}={{0.5}^{\circ }}\left( 60\times H\times M \right)$ and ${{\theta }_{m}}={{6}^{\circ }}\times M$ where ${{\theta }_{h}},{{\theta }_{m}}$ are the angle of our hand and minute hand measured clockwise from 12 o’clock positions, $H$ is the hour and $M$ is the minute passed hour.