Question

At a certain time a tree $6m$ high casts a shadow of length $8m$. At the same time, a pole casts a shadow of length $20m$. Find the height (meters) of the pole.

Answer 1

Hint:Draw a figure which will help you visualize the question properly. Assume the pole and tree to be perpendicular to the ground. Remember that the rays from the Sun are always parallel. Use all the given information to prove the similarity between the triangles. The corresponding sides of a similar triangle are in the same ratio.


Complete step-by-step answer:

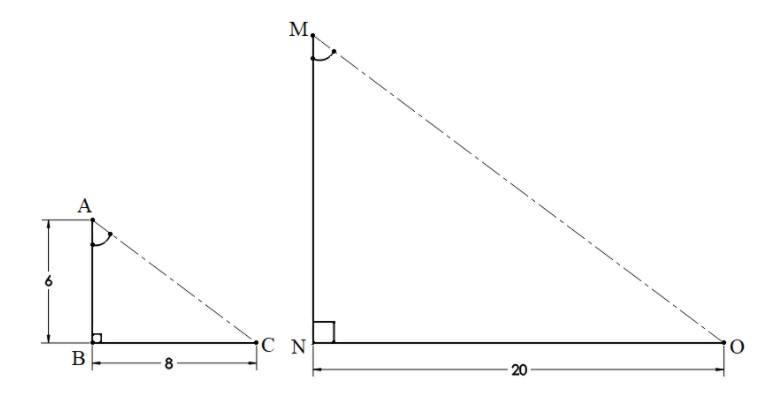
Let’s try to visualize the conditions given in the question by using a diagram.
We can take a tree, say $AB$, of length $6m$ and the shadow which it casts on the ground as $BC$ , of length $8m$.
This will give you a triangle $\Delta ABC$. Similarly, we can draw a triangle $\Delta MNO$ where the pole is $MN$ and its shadow is $NO$ , with a length of $20m$, as shown in the above figure.
Before going further, you must understand a few things are taken under consideration for solving such questions. Firstly, we always assume the light rays coming from the Sun as parallel lines since the distance between the Sun and the Earth is so large and distance from the tree to pole is negligible in respect to that. And also the tree and pole are making a right angle with the ground, i.e. their shadow.
Therefore, from the above assumptions, we can imply that:
$ \Rightarrow \angle ABC = \angle MNO = 90^\circ $ and $AC\parallel MO$
Since the parallel line make the same angle with perpendicular$ \Rightarrow \angle BAC = \angle NMO$
So, now we have two of three angles equal to each other in the triangles $\Delta ABC$ and $\Delta MNO$, thus the third angle should also be equal to each other since the sum of all the angles is $180^\circ $.
By using AAA similarity rules in the triangles $\Delta ABC$ and $\Delta MNO$, which states that if two triangles have three angles equal then the triangles are similar.
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion. In other words, similar triangles are the same shape, but not necessarily the same size.
$ \Rightarrow $ For similar triangles $\Delta ABC$ and $\Delta MNO$, $\dfrac{{AB}}{{MN}} = \dfrac{{BC}}{{NO}}$
Now, let’s substitute the known values in the above relation:
$ \Rightarrow \dfrac{{AB}}{{MN}} = \dfrac{{BC}}{{NO}} \Rightarrow \dfrac{6}{{MN}} = \dfrac{8}{{20}}$
This above equation can be easily solved for the value of $MN$
$ \Rightarrow \dfrac{6}{{MN}} = \dfrac{8}{{20}} \Rightarrow MN = \dfrac{{20 \times 6}}{8} = 15m$
Hence, the length of the pole $MN$ is $15m$.

Note:Try to make a rough figure before starting the calculations. Carefully relate the corresponding side of the similar triangle. An alternate approach can be taken by using the two same angles and consider the similarity rule AA.