Question

At what angle diagonals of a square intersect each other ?

Answer 1

Hint: Here in this question, we need to find the angle in intersection point of two diagonals in the square. For this first we need to draw a shape of square and two diagonals then we can measure or identify an angle made when two diagonals meet or intersect the point of two diagonals.

Complete step-by-step solution:
Square is a regular quadrilateral or four-sided polygon, which has all the four sides of equal length in measurement and all four angles are also equal. The angles at the corner of the square are at right-angle or equal to 90-degrees.
Diagonal is a straight line connecting two non-adjacent angles or vertices of a polygon or shapes of geometry.
In square, the length of the diagonals are equal and bisect each other at $${90^ \circ }$$.
Now consider the Square ABCD all sides of the square are equal length i.e., AB = BC = CD = AD.
In square ABCD, AD and BC are the diagonals and ‘O’ be the intersection point of two diagonals AD and BC.

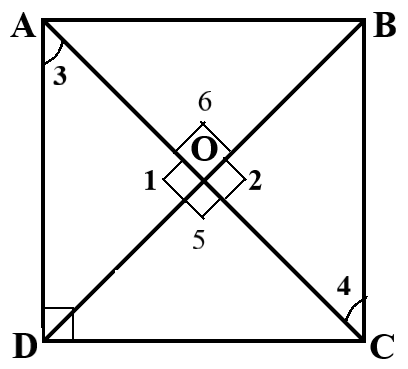
In square $$ABCD$$
Consider triangles $$\vartriangle \,ADC$$ and $$\vartriangle \,BDC$$
In $$\vartriangle \,ADC$$ and $$\vartriangle \,BDC$$
$$AD = BC$$ ($$\because $$ sides of square)
$$DC = DC$$ ($$\because $$Common sides)
$$\angle \,ADC = \angle \,BCD$$ (each angle by $${90^ \circ }$$)
$$ \Rightarrow \,\,\vartriangle \,ADC \cong \,\,\vartriangle \,BDC$$ (By Side angle Side i.e., SAS axiom)
$$ \Rightarrow \,\,AC = BD$$ (By theorem Corresponding parts of congruent triangles i.e., C.P.C.T )
In $$\vartriangle \,AOD$$ and $$\vartriangle \,BOC$$
$$\angle \,1 = \angle \,2$$ (Vertically opposite angles)
$$\angle \,3 = \angle \,4$$ (alternate angles)
$$AD = BC$$ (Given)
$$ \Rightarrow \,\,\vartriangle \,AOD \cong \,\,\vartriangle \,BOC$$ (By Angle Angle Side i.e., AAS axiom)
$$ \Rightarrow \,\,AO = OC$$ and $$BO = OD$$ (By theorem Corresponding parts of congruent triangles i.e., C.P.C.T )
In $$\vartriangle \,DOC$$ and $$\vartriangle \,BOC$$
$$DC = BC$$ ($$\because $$ sides of square)
$$BO = OD$$ (Already proved)
$$OC = OC$$ ($$\because $$Common sides)
$$ \Rightarrow \,\,\vartriangle \,DOC \cong \,\,\vartriangle \,BOC$$ (By Side Side Side i.e., SSS axiom)
$$ \Rightarrow \,\,\,\angle \,5 = \angle \,2$$ (By C.P.C.T)
$$ \Rightarrow \,\,\angle \,5 = \angle \,6$$ (Vertically opposite angles)
$$ \Rightarrow \,\,\angle \,2 = \angle \,6$$ (By linear pair axiom)
In line AC
$$ \Rightarrow \,\,\,\angle \,2 + \angle \,6 = {180^ \circ }$$
By the above information
$$ \Rightarrow \,\,\,\angle \,2 + \angle \,2 = {180^ \circ }$$
$$ \Rightarrow \,\,\,2\angle \,2 = {180^ \circ }$$
Divide both side by 2, then we get
$$ \Rightarrow \,\,\,\angle \,2 = \dfrac{{{{180}^ \circ }}}{2}$$
$$\therefore \,\,\,\,\,\angle \,2 = {90^ \circ } = \angle \,6$$
$$\angle \,5 = \angle \,6 = {90^ \circ }$$ (vertically opposite angles)
$$\angle \,1 = \,\angle \,2 = {90^ \circ }$$ (vertically opposite angles)
$$\therefore \,\,\,\angle \,1 = \,\angle \,2 = \angle \,5 = \angle \,6 = {90^ \circ }$$
$$\therefore \,\,\,\,\,\,\,\,\angle \,AOD = \angle \,AOB = \angle \,BOC = \angle \,COD = {90^ \circ }$$
Therefore, at $${90^ \circ }$$ angle or right angle, the diagonals of a square intersect each other.

Note: While solving these type of questions, we have to know the some basic properties, Axiom and postulates of triangle like when two triangles are congruent all sides and angles of two triangles should be equal, when if two triangles are similar the corresponding sides are in proportion and the corresponding angles are congruent and know about postulates like SAS, ASA, AAA etc…