Question

At what angle must two forces \[(x+y)\text{ and (}x-y)\] act so that the resultant force will be \[\sqrt{{{x}^{2}}+{{y}^{2}}}\]?

Answer 1

Hint: It is given that the two forces act in an angle such that its magnitude is a known fixed value. To solve this, we need to use the equations that give the magnitude of two or more vector quantities and substitute all the forces and find the angle involved.

Complete step-by-step solution

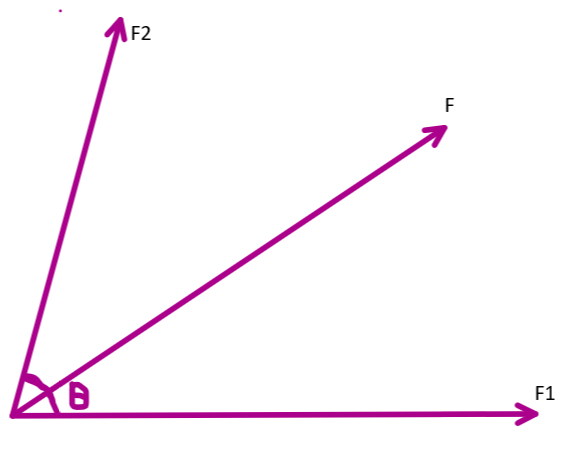
We know that any vector quantities can be added or subtracted by using the angle involved between them and the magnitudes using triangle law of parallelogram law of vector addition. We can just find the magnitude and direction also by means of equations derived from these laws.
Let us consider \[{{Z}_{1\text{ }}}\text{and }{{Z}_{2}}\]as two vectors. They are acting at an angle \[\theta \] with each other. For such a case, the resultant of the two vectors ‘Z’ is given by -
i.e., \[Z=\sqrt{{{Z}_{1}}^{2}+{{Z}_{2}}^{2}+2{{Z}_{1}}{{Z}_{2}}\cos \theta }\]
Thus, we can find the resultant of any two vectors with a given angle. Now, what happens when the resultant vector is given and we need to find the angle at which these vectors act so that they have a required resultant vector. It is very easy to find the angle from the cosine function, which follows.
Let us consider two forces as given in the question as –
\[{{F}_{1}}=(x+y)\text{ and }{{\text{F}}_{2}}\text{=(}x-y)\]
The magnitude of the resultant of two forces can be given by –
\[F=\sqrt{{{F}_{1}}^{2}+{{F}_{2}}^{2}+2{{F}_{1}}{{F}_{2}}\cos \theta }\]
Here, we are given that
\[{{F}_{1}}=(x+y)\text{ and }{{\text{F}}_{2}}\text{=(}x-y)\],
\[\begin{align}
  & \Rightarrow \text{ }F=\sqrt{{{(x+y)}^{2}}+{{(x-y)}^{2}}+2(x+y)(x-y)\cos \theta } \\
 & \Rightarrow \text{ }F=\sqrt{2{{x}^{2}}+2{{y}^{2}}+(2{{x}^{2}}-2xy+2xy-2{{y}^{2}})\cos \theta } \\
\end{align}\]
But it is already given that,
\[\begin{align}
  & F=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
 & \Rightarrow \text{ }\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{2{{x}^{2}}+2{{y}^{2}}+(2{{x}^{2}}-2xy+2xy-2{{y}^{2}})\cos \theta } \\
 & \Rightarrow \text{ }{{\text{x}}^{2}}+{{y}^{2}}=2{{x}^{2}}+2{{y}^{2}}+(2{{x}^{2}}-2{{y}^{2}})\cos \theta \\
 & \Rightarrow \text{ }{{x}^{2}}+{{y}^{2}}+(2{{x}^{2}}-2{{y}^{2}})\cos \theta =0 \\
 & \Rightarrow \text{ }\cos \theta =\dfrac{-({{x}^{2}}+{{y}^{2}})}{2({{x}^{2}}-{{y}^{2}})} \\
 & \Rightarrow \text{ }\theta ={{\cos }^{-1}}(\dfrac{-({{x}^{2}}+{{y}^{2}})}{2({{x}^{2}}-{{y}^{2}})}) \\
\end{align}\]
This is the required angle at which the force should act.
Additional Information: The magnitude of a resultant vector is dependent on the angle between two or more vectors.

Note: This is the simplest method of calculating the required angle for the resultant force. We can use diagram interpretation and vector summing using the unit vectors to find the answer which is tedious and may produce wrong solutions if not considered seriously.