
Banking of roads is provided at turns to:
A. Reduce inertia
B. Increase centripetal force
C. Increase fiction
D. None of these
Answer
513k+ views
Hint: Banking of roads is done at curves i.e. when roads come across circular paths. Now two forces act on a body when it undergoes a circular motion, namely centripetal and centrifugal forces. The centrifugal force acts outward from the center while centripetal force is directed inwards ensuring that the body stays in the curved path.
Complete step by step answer:
When vehicles go through a turn they travel about a nearly circular arc. Thus there must be some force that produced the required acceleration. If the vehicle goes in a horizontal circular path, this resultant force is also horizontal.
Consider a situation as shown below, a vehicle of mass M is moving at a speed v making a turn on the circular path of radius r. So the external forces acting on the vehicle are
Weight of the vehicle, Mg
Normal force, N
Friction,
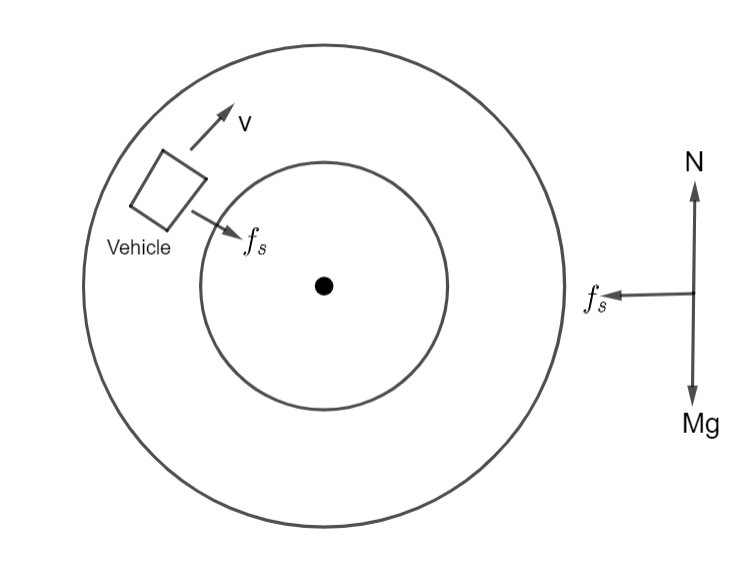
If the road is horizontal, the normal force N is vertically upwards. The only horizontal force that can act towards the center is the friction
However, there is a limit to the magnitude of the frictional force. Thus friction is not always reliable if high speed and sharp turns are involved. So to avoid dependence on the friction, the roads are banked at a turn so that the outer part of the road is somewhat lifted up in comparison to the inner part. In return this changes the angle for the normal reaction force N, creating a component of this force along the radius of the road and towards the center. This additional force provides the sufficient centripetal force to overcome skidding of the vehicle.
Therefore, the correct option is B. i.e., increase centripetal force.
Note: If
Complete step by step answer:
When vehicles go through a turn they travel about a nearly circular arc. Thus there must be some force that produced the required acceleration. If the vehicle goes in a horizontal circular path, this resultant force is also horizontal.
Consider a situation as shown below, a vehicle of mass M is moving at a speed v making a turn on the circular path of radius r. So the external forces acting on the vehicle are
Weight of the vehicle, Mg
Normal force, N
Friction,

If the road is horizontal, the normal force N is vertically upwards. The only horizontal force that can act towards the center is the friction
However, there is a limit to the magnitude of the frictional force. Thus friction is not always reliable if high speed and sharp turns are involved. So to avoid dependence on the friction, the roads are banked at a turn so that the outer part of the road is somewhat lifted up in comparison to the inner part. In return this changes the angle for the normal reaction force N, creating a component of this force along the radius of the road and towards the center. This additional force provides the sufficient centripetal force to overcome skidding of the vehicle.
Therefore, the correct option is B. i.e., increase centripetal force.
Note: If
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




