
Banking of the roads is done due to
A.)Provide enough friction for circular motion of the vehicle
B.)Provide necessary centripetal force required for circular motion of the vehicle
C.)Provide enough radius of curvature for circular motion of the vehicle
D.)Provide enough area for navigating in the circular motion of the vehicle
Answer
515.1k+ views
Hint: When we go around a curved path we need some force to act as centripetal force to prevent us from sliding. When the roads are banked, a component of normal from the road can act as a centripetal force. Thus ensuring safe ride even at higher speed.
Complete step by step answer:
Let us consider a scenario in which a car is going around a curved path and the road is flat. Here, only frictional force will provide centripetal acceleration. Centripetal acceleration is proportional to square of velocity of the object (here, a car). So friction will force will have to increase for greater velocities, but it has some limitations and cannot exceed beyond a value. So there will exist a velocity beyond which the car will not be able to go through the curved path and eventually skid. This value of velocity is equal to
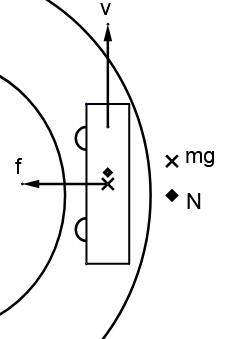
Now, if the road is banked in addition to friction there will be a component of normal from the road which will aid in providing this centripetal force. So now the limiting value of velocity beyond which the car will not be able to go through the curved path, will increase. This value of velocity is equal to
Hence the correct option is B.
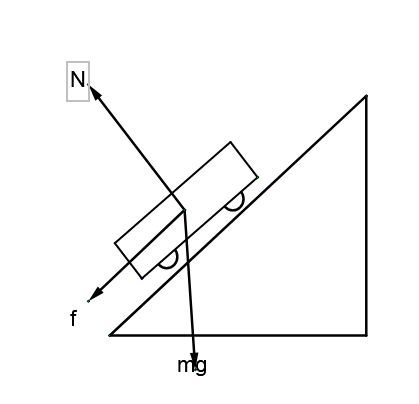
Note: Some students might find that after banking only a component of friction is acting as centripetal force, however before banking complete friction was acting as centripetal force. But even after taking that into consideration, calculations have shown that limiting velocity after banking is much greater than limiting velocity before banking. Also after banking a minimum velocity should also be maintained else car will slip down; however there is no such limit for unbanked roads
Complete step by step answer:
Let us consider a scenario in which a car is going around a curved path and the road is flat. Here, only frictional force will provide centripetal acceleration. Centripetal acceleration is proportional to square of velocity of the object (here, a car). So friction will force will have to increase for greater velocities, but it has some limitations and cannot exceed beyond a value. So there will exist a velocity beyond which the car will not be able to go through the curved path and eventually skid. This value of velocity is equal to

Now, if the road is banked in addition to friction there will be a component of normal from the road which will aid in providing this centripetal force. So now the limiting value of velocity beyond which the car will not be able to go through the curved path, will increase. This value of velocity is equal to
Hence the correct option is B.

Note: Some students might find that after banking only a component of friction is acting as centripetal force, however before banking complete friction was acting as centripetal force. But even after taking that into consideration, calculations have shown that limiting velocity after banking is much greater than limiting velocity before banking. Also after banking a minimum velocity should also be maintained else car will slip down; however there is no such limit for unbanked roads
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




