Question

BE and CF are two equal altitudes of a triangle ABC. Using the RHS congruence rule, prove that the triangle ABC is isosceles.

Answer 1

Hint: An altitude is always perpendicular from the base to the opposite vertex.
A triangle is a polygon with three edges and three vertices, which are the basic shapes in geometry. It is a closed two-dimensional shape with three straight sides.
A triangle has three sides, and their type depends on the length of its sides and the size of its angles. There are basically three types of a triangle based on the length of the sides, namely: Scalene Triangle, Isosceles Triangle, and Equilateral Triangle.
An isosceles triangle is a triangle that has two sides of equal length. All the three angles of the isosceles triangle are acute angle, i.e., less than,\[{90^ \circ }\]whereas its total sum of internal angle is \[{180^ \circ }\]

Complete step-by-step answer:
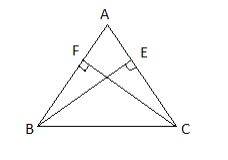
Given BE is the altitude, line BE is drawn from vertex B, and it joins the side AC
So \[\angle AEB = \angle CEB = {90^ \circ } - - - (i)\]
[Since the line is drawn from a line to the opposite vertex are always perpendiculars at its base]
Also, CF is the altitude, line CF is drawn from vertex C, and it joins the side AB
Therefore, \[\angle AFC = \angle BFC = {90^ \circ } - - - (ii)\]
[Since the line is drawn from a line to the opposite vertex are always perpendiculars at its base]
Also, BE=FC
Now consider the triangle \[\vartriangle BFC\]and \[\vartriangle CBE\]
Here \[\angle BFC = \angle CEB = {90^ \circ }\][Since both are\[{90^ \circ }\]]
\[BC = CB\][Common side]
\[FC = EB\][Given]
Since three conditions are satisfied, hence
\[\vartriangle BFC \cong \vartriangle CEB = {90^ \circ }\][RHS congruence rule]
\[\therefore \angle FBC = \angle ECB\] [CPCT]
So we can write
\[\angle ABC = \angle ACB\]
Since the two angles are equal, hence we can say
\[AB = AC\][Side opposite to equal angles is equal]
Hence \[\vartriangle ABC\]is an isosceles triangle
Hence proved

Note: Students must note that whenever an angle for two triangles is common, then the angle is known as a common angle, and it fulfills one condition to equate two triangles.