Question

How many bricks will be required to construct a wall 10m long 4m wide and 3m high, if each brick measures 25cm \[\times \] 12cm \[\times \] 8cm.

Answer 1

Hint:
 Assume L, B and H as the length, breadth and height of the wall which is to be constructed. Similarly, assume l, b and h as the length, breadth and height of one brick that is being used to construct the wall. Assume that the total number of bricks required is ‘n’. Now, use the volume relation given as: - Volume of wall = n \[\times \] volume of one brick, to determine the value of n. Use the formula for volume of a cuboid given as: - Volume = length \[\times \] breadth \[\times \] height.

Complete step by step answer:
Here, we have been provided with the dimensions of a wall that is to be constructed with many bricks whose dimensions are provided. We have to determine the number of bricks that will be needed to construct the wall.
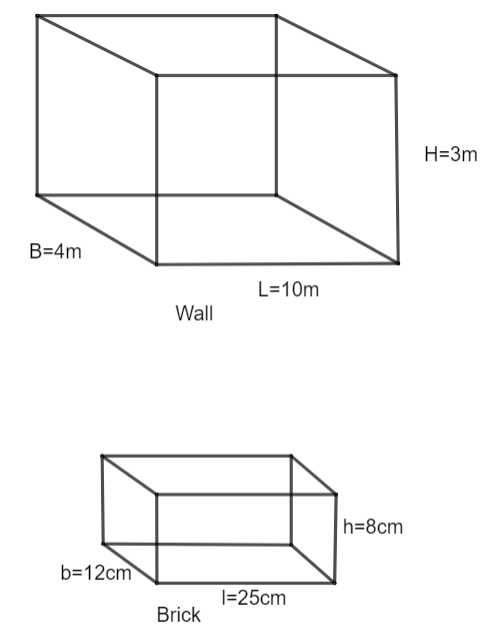
Now, let us assume L, B and H as the length, breadth and height of the wall and l, b and h as the length, breadth and height of each brick needed. So, we have,
L = 10m, B = 4m, H = 3m
l = 25cm, b = 12cm, h = 8cm
Let us convert the dimensions of brick given in cm into m. We know that: - 100cm = 1m, so we have, 1 cm = \[\dfrac{1}{100}\]m. So, the dimensions of each brick can be given as: -
\[\Rightarrow l=\dfrac{25}{100}m,b=\dfrac{12}{100}m,h=\dfrac{8}{100}m\]
Now, we know that each brick will be cuboidal in shape and the same will be the shape of the wall. So, what we are doing is actually we are filling a big cuboid-shaped object with several small cuboid-shaped objects.

Let's assume the total number of bricks required to construct the wall is ‘n’. So, these ‘n’ bricks will occupy all the space required to construct the wall of given dimensions. For this to happen, the volume of wall to be constructed must be equal to the total volume of these ‘n’ bricks. So, using the required volume relation, we get,
\[\Rightarrow \] Volume of wall = n \[\times \] volume of one brick
Applying the formula for the volume of cuboid given as: -
Volume = length \[\times \] breadth \[\times \] height, we get,
\[\Rightarrow \] L \[\times \] B \[\times \] H = n \[\times \] l \[\times \] b \[\times \] h
Substituting the values of L, B, H, l, b and h in the above relation, we get,
\[\begin{align}
  & \Rightarrow 10\times 4\times 3=n\times \dfrac{25}{100}\times \dfrac{12}{100}\times \dfrac{8}{100} \\
 & \Rightarrow n=\dfrac{10\times 4\times 3\times 100\times 100\times 100}{25\times 8\times 12} \\
 & \Rightarrow n=10000 \\
\end{align}\]
Hence, we will need 10000 bricks to construct the wall with provided dimensions.
Note:
One may note that we have converted the dimensions of brick given in cm into m. This is done because, to perform mathematical operations like addition, subtraction, multiplication or division the units of the quantities provided must be the same. You may also convert the dimensions of the wall given in m into cm leaving the dimensions of brick as it is. This process will also give the same value of n. Now, remember that we have to fill the space and not area that is why we have used the volume relation. If we will use the area relation then we will get the wrong answer.