Question

Calculate angle of friction between wedge and block system is at rest. Coefficient of friction between the wedge and block is $ \mu $ .

 $ \begin{align}
  & \text{A}\text{. ta}{{\text{n}}^{-1}}\mu \\
 & \text{B}\text{. }2\theta \\
 & \text{C}\text{. }\theta \\
 & \text{D}\text{. }\dfrac{\theta }{2} \\
\end{align} $

Answer 1

Hint: For a block being placed on an inclined plane, different forces acting on the block are: Gravitational force, Normal force, and Frictional force. We will draw the force body diagram for the block and will determine the angle of friction between block and wedge. For the block to be at rest, all the forces acting on the block should be balanced, both in the direction parallel and perpendicular to the inclined plane.

Formula used:
Relation between frictional force and normal reaction,
 $ f=\mu N $

Complete step-by-step answer:
Motion of a block on an inclined plane is the interplay of different force types and the characterising features of the inclined plane. An inclined plane is a surface whose one end is raised. The raised surface forms angle $ \theta $ with the horizontal. The block placed on the inclined surface is acted upon by the force of gravity and contact forces, normal force and frictional force.
Forces acting on the block of mass $ m $ are:
Gravitational force $ mg $ in downward direction,
Components of the gravitational force will be:
 $ mg\cos \theta $ in the direction parallel to the inclined plane and $ mg\sin \theta $ in the direction perpendicular to the inclined plane
Frictional force $ f $ in the direction opposite to the tending motion of the block
Force-body diagram (FBD) of block:

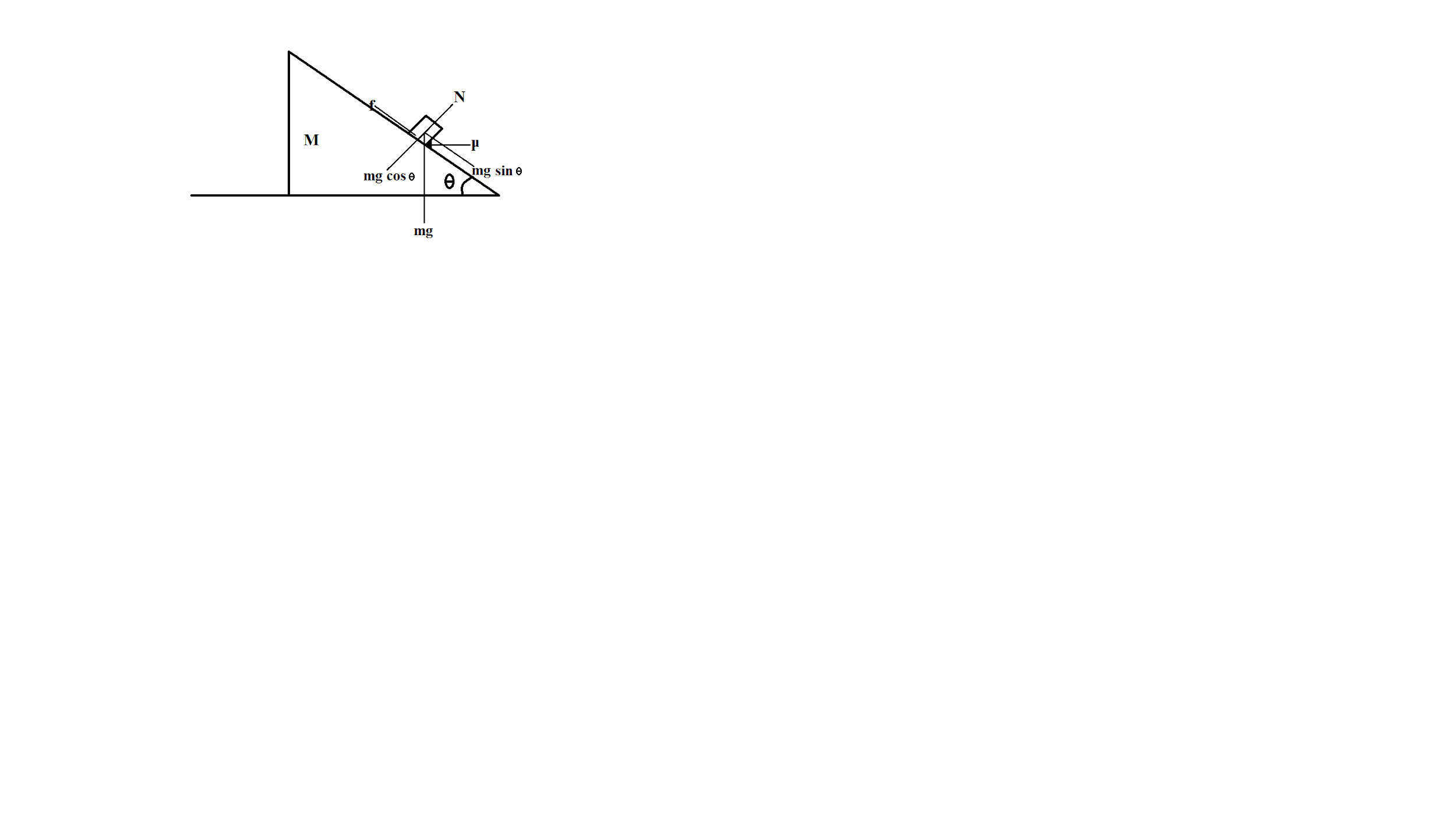
As we are given that the system is at rest,
It means that all the forces on the block are balancing each other.
In direction perpendicular to the inclined plane, we have Normal force $ N $ and component of gravitational force $ mg\cos \theta $
These two forces will balance each other,
 $ N=mg\cos \theta $
In direction perpendicular to the inclined plane, we have frictional force $ f $ and component of gravitational force $ mg\sin \theta $
These two forces will balance each other,
 $ f=mg\sin \theta $
We have,
 $ f=\mu N $
Where,
 $ f $ is the frictional force
 $ \mu $ is the coefficient of friction
 $ N $ is the normal force
And, $ N=mg\cos \theta $
 $ \begin{align}
  & \mu N=mg\sin \theta \\
 & \mu mg\cos \theta =mg\sin \theta \\
 & \mu =\dfrac{\sin \theta }{\cos \theta } \\
 & \mu =\tan \theta \\
 & \theta ={{\tan }^{-1}}\mu \\
\end{align} $
The angle of friction between the block and the wedge is $ {{\tan }^{-1}}\mu $
Hence, the correct option is A.

Note: While making the force body diagram of an object placed on an inclined plane, all the forces should be considered and drawn carefully along the right direction. For an object to be at rest, the forces should be balanced in all the directions. Normal or reaction force always acts perpendicular to the surface of contact and frictional force is acted along the surface of contact.