Question

Calculate angular momentum of a satellite with respect to centre of earth if mass of satellite is ‘m’ and radius of orbit is ‘r’ and mass of earth is ‘M’

Answer 1

Hint: It is said that there is a satellite orbiting the earth. We have an equation to find the angular momentum of a satellite with respect to the centre of earth. And we also have an equation to find the orbital velocity of a satellite. By substituting this in the equation for angular momentum, we get the solution.
Formula used:
Angular momentum, $\vec{L}=r\times \vec{p}$

Complete answer:
We are given a satellite in the question.
It is said that the mass of the satellite is ‘m’, radius of the orbit is ‘r’ and mass of earth is considered as ‘M’.
The figure below shows the given situation.

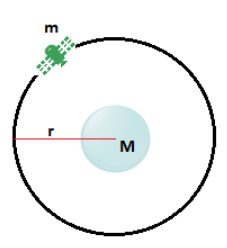
We have earth in the centre and a satellite revolving around earth in an orbit with radius ‘r’.
We are asked about the angular momentum of the satellite with respect to the centre of earth.
We know that the equation for angular momentum is given by,
$\vec{L}=r\times \vec{p}$, where ‘L’ is angular momentum, ‘r’ is radius and ‘p’ is momentum.
We know momentum is given by,
$\vec{p}=mv$, where ‘m’ is mass of the body and ‘v’ is velocity of the body.
Therefore we get angular momentum as
\[\Rightarrow \vec{L}=m\vec{v}r\]
In the given case, mass is the mass of the satellite ‘m’, radius is the radius of the orbit ‘r’ and velocity is the orbital velocity.
We know that orbital velocity of a satellite is given by the equation,
$v=\sqrt{\dfrac{GM}{r}}$, where ‘G’ is gravitational constant, ‘M’ is mass of earth and ‘r’ is radius of the orbit.
By substituting this in the equation of angular momentum, we get
$\Rightarrow \vec{L}=mr\times \sqrt{\dfrac{GM}{r}}$
By squaring on both sides,
$\Rightarrow {{L}^{2}}={{m}^{2}}{{r}^{2}}\dfrac{GM}{r}$
By solving this equation, we get
$\Rightarrow {{L}^{2}}={{m}^{2}}rGM$
Therefore,
$\Rightarrow \vec{L}=m\sqrt{GMr}$
Hence the angular momentum of a satellite with respect to centre of earth is,
$\vec{L}=m\sqrt{GMr}$

Note:
Angular momentum of a body is simply the total amount of rotational motion of that body. Angular momentum is experienced by bodies mainly in two situations; when the body is accelerating about a fixed point and when the body is rotating about a fixed point.
Angular momentum when the body is accelerating about a fixed point is given as,
$\vec{L}=r\times \vec{p}$
Angular momentum when the body is rotating about a fixed point is given as,
$\vec{L}=I\times \vec{\omega }$