Question

Calculate heat absorbed by a system is going through the cyclic process as shown in the figure.

Answer 1

Hint: In a cyclic process, the internal energy in a cycle remains constant. This makes the change in the internal energy of the system zero. This means that the heat absorbed by the system is fully used to do the work. Thus, the area of this curve gives us the heat absorbed by the system.

Complete Step by step solution:
In the question, it is given that,
The process is cyclic, therefore the change in internal energy is zero. This makes the total heat absorbed by the system equal to the area of the curve formed by the P-V curve.
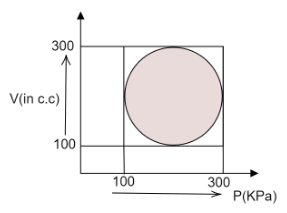
From the figure, we can deduce that,
The minimum volume of the system, $ {V_i} = 100cc $
The maximum volume of the system, $ {V_f} = 300cc $
The minimum pressure of the system, $ {P_i} = 100KPa $
The maximum pressure of the system, $ {P_f} = 300KPa $
This gives, the difference between the maximum and minimum pressure,
 $ \Delta P = {P_f} - {P_i} $
 $ \Delta P = 300 - 100 $
 $ \Delta P = 200KPa $
And the difference between the maximum and minimum volume,
 $ \Delta V = {V_f} - {V_i} $
 $ \Delta V = 300 - 100 $
 $ \Delta V = 200cc $ or $ c{m^3} $
The range of pressure and volume change is equal,
Therefore, the curve traced by the cyclic process is circular.
We know that the area of a circle is,
 $ A = \pi {r^2} $
The difference between the minimum and maximum value gives the diameter of the circle formed by the curve.
Therefore the radius of the circle,
  $ r = \dfrac{d}{2} $
The area enclosed by the graph is given by,
 $ A = \pi \left( {\dfrac{{\Delta V}}{2}} \right)c{m^3} \times \left( {\dfrac{{\Delta P}}{2}} \right)KPa $
Keeping the values,
 $ A = \pi \left( {\dfrac{{200}}{2}} \right)c{m^3} \times \left( {\dfrac{{200}}{2}} \right)KPa $
 $ \Rightarrow A = \pi \times 100c{m^3} \times 100KPa $
 $ \Rightarrow A = 3.14 \times {10^4}\left( {c{m^3} \times KPa} \right) $
The units $ c{m^3} $ and $ \;KPa $ are not the SI unit values of volume and Pressure, thus, to get the answer in joules, we convert them into SI units.
We know that,
 $ 1c{m^3} = {10^{ - 6}}{m^3} $
And, $ 1KPa = {10^3}Pa $
Substituting these values in the area of the curve, we get-
 $ A = 3.14 \times {10^4} \times {10^{ - 6}} \times {10^3}\left( {{m^3} \times Pa} \right) $
 $ A = 3.14 \times 10{m^3}Pa $
Or
 $ A = 31.4J $
This is equal to the heat absorbed during the process,
 $ \Delta H = 31.4J $
The heat absorbed during this cyclic process is $ 31.4\;J $

Note:
Change in internal energy is independent of the path taken by the process. Which means that no matter what path is followed, change in internal energy will only be the difference of initial and final values. Whereas, the energy absorbed or given by the system is path-dependent. This is why, at the end of a cyclic process, there is a change in the heat but no change in the internal energy.