Question

How do you calculate the acceleration of a rocket?

Answer 1

Hint: First, calculate the impulse, i.e., the change in momentum of the rocket in terms of masses and velocities and equate it with $\vec{F}\Delta t$ , as this is the impulse if $\vec{F}$ be the external force on the rocket. Now, from this equation, we can get the acceleration of the rocket.

Complete step by step answer:
A rocket is a device that moves forward by expelling particles of a fuel mixture backward. One of the important uses of a rocket is to put a satellite into an orbit, apart from the interplanetary travels and carrying war-heads.
The principle behind the rocket propulsion is the conservation of momentum. The rocket carries with it both the fuel and the oxidising agent necessary for combustion. The burning of the fuel takes place in a combustion chamber within the rocket system. As the rocket is fired, the exhaust gasses rush backward with a tremendous speed and the rocket is pushed forward by the reaction. Thus the thrust of the rocket is provided by the reaction forces of the high speed gasses ejected at the rear of the rocket.
Let, $m$ be the total mass of the rocket (mass of rocket $+$mass of fuel) at time$t$ and let at a later time $t+\delta t$ , the mass becomes $m+\Delta m$ due to expulsion of a mass $-\Delta m$ of gas at the rear end of the rocket. Since $\Delta m$ is assumed negative, $-\Delta m$ is in fact a positive quantity. Suppose the velocities of the rocket at times $t$ and $t+\Delta t$ relative to an inertial frame with origin $O$ be $\vec{v}$ and $\vec{v}+\Delta \vec{v}$ . the velocity of the ejected mass of the gas relative to $O$ is $\vec{v}+\vec{u}$ where $-\vec{u}$ is the velocity of the gas relative to the rocket.

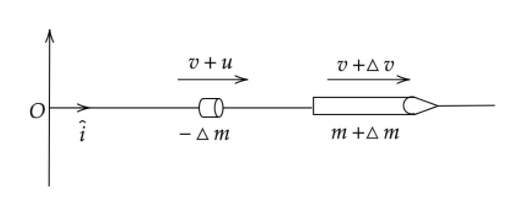
Therefore, impulse = change in momentum of the system
= total momentum at $(t+\Delta t)$ $-$ total momentum at $t$
= $[(m+\Delta m)(\vec{v}+\Delta \vec{v})+(-\Delta m)(\vec{v}+\vec{u})]-m\vec{v}$
Now, if $\vec{F}$ is the external force acting on the rocket, then the impulse is $\vec{F}\Delta t$ .
So, $[(m+\Delta m)(\vec{v}+\Delta \vec{v})+(-\Delta m)(\vec{v}+\vec{u})]-m\vec{v}=\vec{F}\Delta t$
Or, $[(m\vec{v}+m\Delta \vec{v}+\Delta m\vec{v}+\Delta m\Delta \vec{v})+(-\Delta m\vec{v}-\Delta m\vec{u})]-m\vec{v}=\vec{F}\Delta t$
Or, $m\dfrac{\Delta \vec{v}}{\Delta t}-\vec{u}\dfrac{\Delta m}{\Delta t}=\vec{F}$ (neglecting the term $\Delta m\Delta \vec{v}$ as it is very small)
Now, in the limit, $\Delta t\to 0$ , we get,
$m\dfrac{d\vec{v}}{dt}-\vec{u}\dfrac{dm}{dt}=\vec{F}$
Taking the directions as,
$\vec{v}=\hat{i}$ , $\vec{u}=-\hat{i}$ ,$\vec{F}=\hat{i}$ , we obtain,
$m\dfrac{dv}{dt}+u\dfrac{dm}{dt}=F$
Or, $ma+u\dfrac{dm}{dt}=F$
Where, $a$ (magnitude of $\vec{a}$ ) is the acceleration of the rocket
So, the acceleration of rocket is, $a=\dfrac{F-u\dfrac{dm}{dt}}{m}$

Note: Acceleration of the rocket increases if there is an increment in the exhaust velocity of the gases relative to the rocket. Also, the faster the rocket burns its fuel, the greater its acceleration and, the smaller the mass of the rocket (the other factors being unchanged), the greater the acceleration.