
Calculate the acceleration of the moon towards the Earth’s centre.
Answer
453k+ views
1 likes
Hint: Recall that the acceleration of the moon towards the Earth’s centre is the centripetal/radial acceleration of the moon. To this end, first determine the revolutionary period of the moon and the distance travelled by the moon in the circular path to arrive at its linear velocity. Then arrive at its appropriate centripetal acceleration acting along the radius of the circular path it describes around the Earth.
Formula Used:
Radial/centripetal acceleration:
Complete answer:
The acceleration of the moon directed towards the earth’s centre is nothing but the acceleration of the moon arising due to the centripetal force of gravitational attraction between the Earth and the moon. In circular motion, we call this as radial acceleration which is essentially the acceleration of the moon along the radius of the circular path it traces as it revolves around the Earth and is directed towards the centre of this circular path, which in this case is the Earth’s centre.
Quantitatively, radial acceleration is given as:
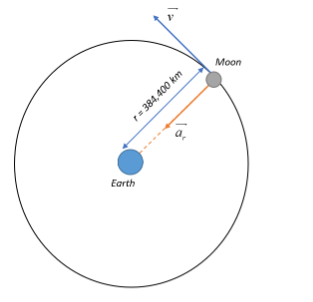
Now, the moon completes one revolution around the Earth in a period of:
and this revolution describes a circular path of radius:
The distance travelled by the moon in describing this circular path will be:
Therefore, the linear velocity with which the moon travels this distance around the Earth can be given as:
The acceleration of the moon towards the Earths’ centre can thus be given as:
Note:
It is important to understand that the radial acceleration of the moon arises from the existence of a gravitational force of attraction between the Earth and the moon. In this case, the acceleration can alternatively be calculated from Newton’s Law of Gravitation as follows:
where gravitational constant
Plugging in the values, we get:
Formula Used:
Radial/centripetal acceleration:
Complete answer:
The acceleration of the moon directed towards the earth’s centre is nothing but the acceleration of the moon arising due to the centripetal force of gravitational attraction between the Earth and the moon. In circular motion, we call this as radial acceleration which is essentially the acceleration of the moon along the radius of the circular path it traces as it revolves around the Earth and is directed towards the centre of this circular path, which in this case is the Earth’s centre.
Quantitatively, radial acceleration is given as:

Now, the moon completes one revolution around the Earth in a period of:
and this revolution describes a circular path of radius:
The distance travelled by the moon in describing this circular path will be:
Therefore, the linear velocity with which the moon travels this distance around the Earth can be given as:
The acceleration of the moon towards the Earths’ centre can thus be given as:
Note:
It is important to understand that the radial acceleration of the moon arises from the existence of a gravitational force of attraction between the Earth and the moon. In this case, the acceleration can alternatively be calculated from Newton’s Law of Gravitation as follows:
where gravitational constant
Plugging in the values, we get:
Latest Vedantu courses for you
Grade 8 | CBSE | SCHOOL | English
Vedantu 8 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




