Question

How do you calculate the actual mechanical advantage of a lever?

Answer 1

Hint: Before we understand the means to calculate the mechanical advantage of a lever, it is important to define the term mechanical advantage, which is given as the measure by which the force amplification can be achieved by the usage of the machine, thereby determining the effectiveness of the machine.

Complete answer:
Lever belongs to the class of simple machines that use the simplest method of amplifying the effort applied by humans into something useful. Lever is one of the six simple machines of the classic age, with the others being: Wheel-and-axle, Pulley, Inclined plane, Wedge and Screw.
Lever consists of a single beam pivoted on a support or a fixed hinge, known as the fulcrum. The load is applied on one extreme end and the effort is applied on the other extreme end, as shown:

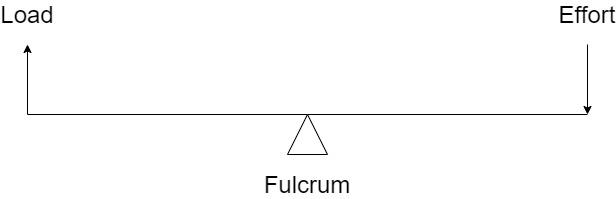Lever is basically employed to obtain the mechanical advantage or leverage, which means the ratio of the force realised by the machine to the force applied on the machine.
Mechanical advantage of the lever is given by –
$MA = \dfrac{{{F_L}}}{{{F_E}}}$
where ${F_E}\& {F_L}$ are efforts and load respectively.
The forces acting on the extreme ends of the lever causes a moment of force about the fulcrum. To establish equilibrium, the total moment of the lever remains constant. This means that the force is directly proportional to the distance of application from the fulcrum.
$\Rightarrow F \propto d$
Thus, we can say
$\Rightarrow \dfrac{{{F_L}}}{{{F_E}}} = \dfrac{{{d_l}}}{{{d_e}}}$
where ${d_l}$ & ${d_e}$ are the distances of the load and effort from the fulcrum, respectively.
Therefore, mechanical advantage is given by –
$\Rightarrow MA = \dfrac{{{d_l}}}{{{d_e}}}$
It so happens that the force applied on the effort end does not necessarily convert entirely to lifting the load. There is loss in the force applied on load due to friction and other factors. Thus, the mechanical advantage in actual cases is lesser than the ideal mechanical advantage that is determined solely by the distances.
Thus,
Ideal Mechanical Advantage, $IMA = \dfrac{{{d_l}}}{{{d_e}}}$
Actual Mechanical Advantage, $AMA = \dfrac{{{F_L}}}{{{F_E}}}$

Note: The ratio of the actual mechanical advantage to the ideal mechanical advantage of the lever is called efficiency of the lever. For example, if the efficiency of a lever is 90%, the actual mechanical advantage is 10% lesser than the ideal mechanical advantage of the lever, wherein the 10% is the loss due to friction and other factors.