Question

Calculate the angle of
( a ) ${{1}^{{}^\circ }}$ (degree)
( b ) $1'$ (minute of arc or arcmin)
( c ) $1''$ ( second of arc or arc second) in radian.
Use ${{360}^{{}^\circ }}=2\pi rad$ , ${{1}^{{}^\circ }}=60'$ and $1'=60''$ .

Answer 1

Hint: For this question what we will do is we will take help of relation between degrees, minutes and seconds with radian measure and will evaluate the value of ${{1}^{{}^\circ }}$ , 1’ and 1” in radians as ${{1}^{\text{ }\!\!{}^\circ\!\!\text{ }}}=\dfrac{2\pi }{360}$ , ${{1}^{{}^\circ }}=60'$ and $1'=60''$.

Complete step-by-step answer:
Before solving let's see what are degree measures and radian measures.

If a rotation from the initial side to terminal side is ${{\left( \dfrac{1}{360} \right)}^{th}}$ revolution, the angle is said to have a measure of on degree written as ${{1}^{{}^\circ }}$and ${{1}^{{}^\circ }}$ is divided into 60 minute and 1 minute is divided into 60 seconds, thus ${{1}^{{}^\circ }}=60'$ and $1'=60''$

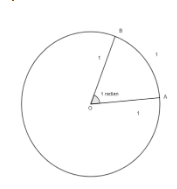
Angles subtended at the centre by an arc of length of 1 unit in a unit circle that is a circle with radius 1 unit is said to have a measure of 1 radian.
Now, relation between degree and radian is $\text{2 }\!\!\pi\!\!\text{ radian=36}{{\text{0}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}$, where $\pi =\dfrac{22}{7}$ or $\pi =3.14$
Now in question we have to find values of ${{1}^{{}^\circ }}$ (degree), $1'$ (minute of arc or arcmin), $1''$ ( second of arc or arc second) in radian.
Now, we know that $\text{2 }\!\!\pi\!\!\text{ radian=36}{{\text{0}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}$
So, taking $\text{36}{{\text{0}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}$ from numerator of right hand side to denominator of left hand side, we get
${{1}^{\text{ }\!\!{}^\circ\!\!\text{ }}}=\dfrac{2\pi }{360}$
On solving we get
${{1}^{\text{ }\!\!{}^\circ\!\!\text{ }}}=\dfrac{\pi }{180}$radian or approximately 0.07146 radian.
Now, we know that ${{1}^{{}^\circ }}=60'$
So, we can write${{1}^{\text{ }\!\!{}^\circ\!\!\text{ }}}=\dfrac{\pi }{180}$ as $60'=\dfrac{\pi }{180}$
Taking 60 from numerator of left hand side to denominator of right hand side, we get
$1'=\dfrac{\pi }{60\times 180}$radians
On solving we get
$1'=0.000291$ radians
Now, we also know that $1'=60''$
So, we can write$60'=\dfrac{\pi }{180}$ as $(60\times 60)''=\dfrac{\pi }{180}$
Taking $60\times 60$ from numerator of left hand side to denominator of right hand side, we get
$1''=\dfrac{\pi }{3600\times 180}$radians
On solving we get
$1''=0.00000485$ radians

Note: For solving these types of questions one must know the relation of degrees, minutes and seconds with radian measure that is ${{1}^{\text{ }\!\!{}^\circ\!\!\text{ }}}=\dfrac{2\pi }{360}$, ${{1}^{{}^\circ }}=60'$ and $1'=60''$. Now, in the calculation part it is not necessary to solve the value of radian by putting the value of $\pi $ but if you solve it be careful of complex calculation.