
Calculate the area and the height of an equilateral triangle whose perimeter is 60 cm.
A.
B.
C.
D.
Answer
525k+ views
Hint:For solving this problem, first we find the side length by using the perimeter. Now, the height of an equilateral triangle is evaluated by using Pythagoras theorem. After this, by using the formula of area of the triangle, we evaluate the area of the equilateral triangle. In this way we can easily solve the problem.
Complete step-by-step answer:
According to the problem statement, the perimeter of an equilateral triangle is 60cm. Let all the three equal sides of the equilateral triangle be a each.
The formula for the perimeter of a triangle is the sum of all the sides. So, by using the formula of perimeter of a equilateral triangle:
Therefore, the side length of the equilateral triangle is 20cm.
Now, by using the property that the median of the equilateral triangle bisects the side, calculate the half length of the side.
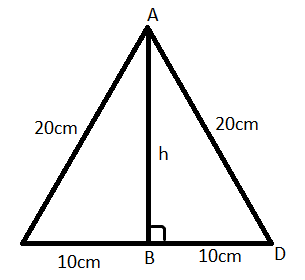
Applying the Pythagoras theorem in triangle ABD,
Therefore, the height of the triangle is 17.32 cm.
Now, the area of a triangle is given by
On putting the values as b = 20 cm and h = 17.32 cm in area, we get
Therefore, the area of the triangle is 173.2 square cm.
Hence, option (C) is correct.
Note: This problem can also be solved alternatively by using the formula for or area of equilateral triangle which can be stated as
Complete step-by-step answer:
According to the problem statement, the perimeter of an equilateral triangle is 60cm. Let all the three equal sides of the equilateral triangle be a each.
The formula for the perimeter of a triangle is the sum of all the sides. So, by using the formula of perimeter of a equilateral triangle:
Therefore, the side length of the equilateral triangle is 20cm.
Now, by using the property that the median of the equilateral triangle bisects the side, calculate the half length of the side.

Applying the Pythagoras theorem in triangle ABD,
Therefore, the height of the triangle is 17.32 cm.
Now, the area of a triangle is given by
On putting the values as b = 20 cm and h = 17.32 cm in area, we get
Therefore, the area of the triangle is 173.2 square cm.
Hence, option (C) is correct.
Note: This problem can also be solved alternatively by using the formula for or area of equilateral triangle which can be stated as
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




