Question

Calculate the area of a circular ring whose outer and inner radii are \[12\] and \[10\ cm\].
A.\[118.16\ cm^{2}\]
B.\[128.16\ cm^{2}\]
C.\[138.16\ cm^{2}\]
D.\[148.16\ cm^{2}\]

Answer 1

Hint: In this question, we need to find the area of a circular ring. A ring is nothing but a space between two concentric circles. Concentric circles are circles with the same centre and different radius. We can find the area of the ring by subtracting the area of the outer circle and area of the inner circle.
Formula used :
\[Area\ of\ the\ circle\ = \pi r^{2}\]
Where \[r\] is the radius of the circle and \[\pi\] is the mathematical constant, values \[3.14\] .

Complete step by step answer:

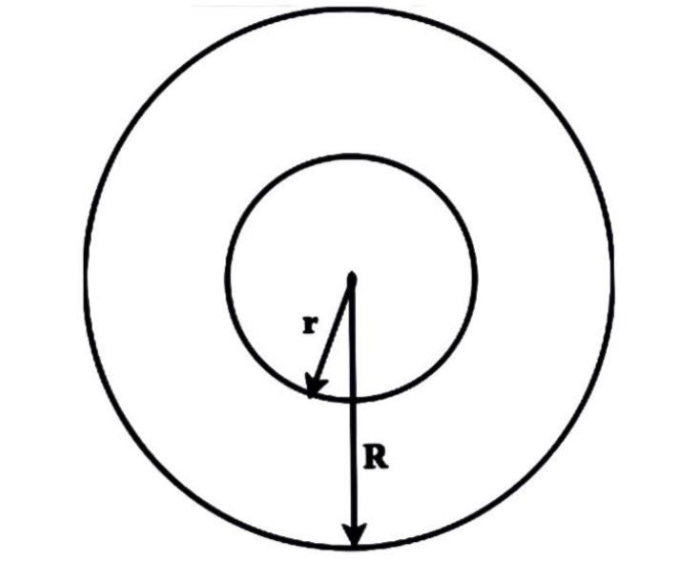
Given, outer and inner radii are \[12\ cm\] and \[10\ cm\] respectively.
Let us consider the radius of the outer circle as \[R\] and the radius of the inner circle as \[r\].
Radius of outer circle ,
\[R = 12\ cm\]
Radius of inner circle,
\[r = 10\ cm\]
We can find the area of the ring by subtracting the area of the outer circle and area of the inner circle.
⇒ \[Area\ of\ the\ ring\ = \ Area\ of\ the\ outer\ circle - \ {Area\ of\ the\ inner\ circle}\]
First we can find the area of the outer circle with radius \[R = 12\ cm\] .
\[Area\ of\ the\ outer\ circle = \pi R^{2}\]
By substituting the values,
We get,
\[Area = 3.14 \times \left( 12 \right)^{2}\]
By multiplying,
We get,
\[Area\ of\ the\ outer\ circle = 452.16\ cm^{2}\]
Now we can find the area of the inner circle with radius \[r = 10\ cm\].
\[Area\ of\ the\ inner\ circle = \pi r^{2}\]
By substituting the values,
We get,
\[Area = 3.14 \times \left( 10 \right)^{2}\]
By multiplying,
We get,
\[{Area}{\ of\ the\ inner\ circle} = 314\ cm^{2}\]
Now we can find the area of the ring,
\[Area\ of\ the\ ring\ = \ Area\ of\ the\ outer\ circle - \ {Area\ of\ the\ inner\ circle}\]
\[Area\ of\ the\ ring = 452.16 – 314\]
By subtracting,
We get,
\[Area\ of\ the\ circular\ ring = 138.16\ cm^{2}\]
Thus we get the area of the circular ring is \[138.16\ cm^{2}\]

So, the correct answer is “Option C”.

Note:
Alternative solution :
We can find the area of the ring by subtracting the area of the outer circle and area of the inner circle.
\[Area\ of\ the\ ring\ = \ Area\ of\ the\ outer\ circle - \ {Area\ of\ the\ inner\ circle}\]
\[Area = \pi R^{2} - \pi r^{2}\]
By taking \[π\] common ,
We get ,
\[Area = \pi\left( R^{2} – r^{2} \right)\]
By substituting the values,
We get,
\[Area = 3.14\left( \left( 12 \right)^{2} - \left( 10 \right)^{2} \right)\]
By simplifying,
We get,
\[Area = 3.14(144 – 100)\]
By subtracting,
We get,
\[Area = 3.14 \times (44)\]
By multiplying,
We get,
\[Area = 138.16\]
Thus we get the area of the circular ring as \[138.16\ cm^{2}\]
We can also find the area of the circular ring in this method.