Question

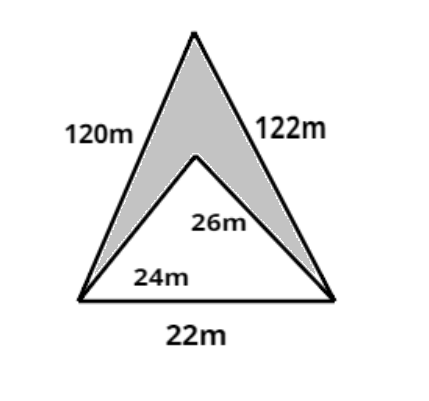
Calculate the area of the shaded region in the given figure.

$
  (a){\text{ 1074}}{{\text{m}}^2} \\
  (b){\text{ 1274}}{{\text{m}}^2} \\
  (c){\text{ 1174}}{{\text{m}}^2} \\
  (d){\text{ 1004}}{{\text{m}}^2} \\
 $

Answer 1

Hint – In this question use the length of the sides given to compute the perimeter of the triangle, then using this perimeter compute the area of the triangles via formula $A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $, where s is the perimeter. The required shaded area will be the area of the larger triangle subtracted with that of the smaller triangle.

Complete Step-by-Step solution:
As we know area (A) of triangle is
$ \Rightarrow A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
Where (s) is half of the perimeter and a, b and c are the sides of the triangle.
So the area (A1) of the bigger triangle is where a = 120m, b= 122m, c = 22m.
$ \Rightarrow s = \dfrac{{a + b + c}}{2} = \dfrac{{120 + 122 + 22}}{2} = 132$meter.
$ \Rightarrow {A_1} = \sqrt {132\left( {132 - 120} \right)\left( {132 - 122} \right)\left( {132 - 22} \right)} = \sqrt {132\left( {12} \right)\left( {10} \right)\left( {110} \right)} = \sqrt {132 \times 132 \times 100} = 1320{\text{ }}{{\text{m}}^2}$Now the area (A2) of the smaller triangle is where a = 24m, b = 26m, c = 22m.
$ \Rightarrow s = \dfrac{{a + b + c}}{2} = \dfrac{{24 + 26 + 22}}{2} = 36$meter.
$ \Rightarrow {A_2} = \sqrt {36\left( {36 - 24} \right)\left( {36 - 26} \right)\left( {36 - 22} \right)} = \sqrt {36\left( {12} \right)\left( {10} \right)\left( {14} \right)} = 245.92{\text{ }}{{\text{m}}^2}$
So the area (A) of the shaded region is the difference of area of bigger triangle and area of smaller triangle.
$ \Rightarrow A = {A_1} - {A_2}$
$ \Rightarrow A = 1320 - 245.92 = 1074.08 \simeq 1074{\text{ }}{{\text{m}}^2}$
So this is the required answer.
Hence option (A) is correct.

Note – In this question the perimeter is calculated using the sides as the perimeter is the sum of all sides, thus we have added all the sides. It is always advised to have a good understanding of the diagrammatic representation in the area problems as it helps figuring out the correct portion to whose area is to be calculated.