
Calculate the relative acceleration of
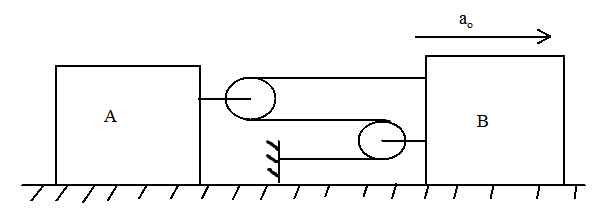

Answer
483k+ views
Hint:First calculate the tensions in all the strings in the figure. Then use the formula which relates tension in string and object’s acceleration to calculate the acceleration of
Formulas Used:
Where,
Complete step by step answer:
First, we will calculate the tension in all the strings. We start from the top. Let the string at the top have a tension
Since tension is always applied away from the body, the same will be the case here. These pulleys/strings do not have any velocity of their own, we can conclude that no net force is acting in them and these tensions are balanced. So, we assume that the same amount of force is acting on all the strings in opposite directions as the tensions we calculated above. The final diagram is shown below.
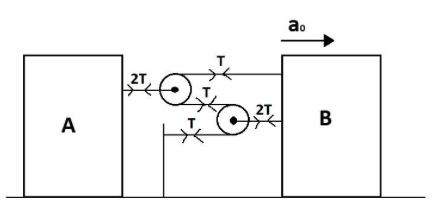
Now we use the formula
On solving this, we get
Transposing,
Or,
We have the acceleration of
This is the required answer.
Note:Tension in a string is always applied away from the body it is attached to. If we do not balance the tension in the string it will mean that force is applied on the string and therefore, the string shall show motion in that direction which is not the case. Hence it is necessary to balance the tensions in the strings.
Formulas Used:
Where,
Complete step by step answer:
First, we will calculate the tension in all the strings. We start from the top. Let the string at the top have a tension
Since tension is always applied away from the body, the same will be the case here. These pulleys/strings do not have any velocity of their own, we can conclude that no net force is acting in them and these tensions are balanced. So, we assume that the same amount of force is acting on all the strings in opposite directions as the tensions we calculated above. The final diagram is shown below.

Now we use the formula
On solving this, we get
Transposing,
Or,
We have the acceleration of
This is the required answer.
Note:Tension in a string is always applied away from the body it is attached to. If we do not balance the tension in the string it will mean that force is applied on the string and therefore, the string shall show motion in that direction which is not the case. Hence it is necessary to balance the tensions in the strings.
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




