Question

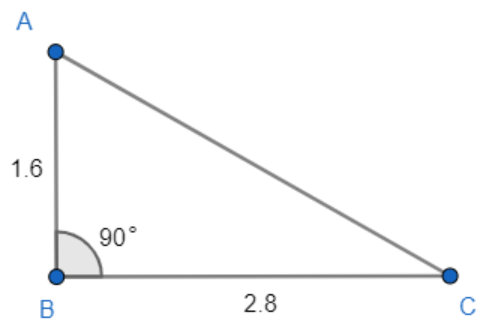
Calculate the size of $\angle BAC$ for the following image.

Answer 1

Hint: We will use the trigonometric identity of $\tan \theta $ for the $\angle BAC$ to find its relation to the sides AB and BC. Then to find the angle we will use the inverse formula of $\tan $.

Complete step by step answer:
For $\vartriangle ABC$, $\angle ABC={{90}^{\circ }}$. So, $\vartriangle ABC$is a right-angled triangle.
$AB=1.6m,\,\,BC=2.8m$.
Let’s assume that $\angle BAC=\alpha $.
Now, with respect to $\angle BAC$, we will take the trigonometric identity of $\tan \alpha $.
So, $\tan \alpha =\dfrac{height}{base}=\dfrac{BC}{AB}$.
The height and base will be considered with respect to $\angle BAC$.
Now, we put the values of AB and BC.
So, $\tan \alpha =\dfrac{BC}{AB}=\dfrac{2.8}{1.6}=\dfrac{7}{4}$.
Thus, from the relation of $\angle BAC$ to the sides AB and BC we got the value of $\tan \alpha $.
Now, we use the inverse theorem of $\tan $to find the value of the angle.
So,
 $\begin{align}
  & \tan \alpha =\dfrac{7}{4} \\
 & \Rightarrow \,\alpha ={{\tan }^{-1}}\left( \dfrac{7}{4} \right) \\
\end{align}$
Thus, we get the value of $\angle BAC$ as $\alpha ={{\tan }^{-1}}\left( \dfrac{7}{4} \right)$.

Note: Even though we didn’t use the side AC at any point in the solution, still we can do that when we are using the identity of $\sin \theta $ and $\cos \theta $. In that case side AC will be considered as the hypotenuse.
so, $\sin \alpha =\dfrac{height}{hypotenuse}=\dfrac{BC}{AC}$ and $\cos \alpha =\dfrac{base}{hypotenuse}=\dfrac{AB}{AC}$.
To find the value of side AC we will use Pythagoras’ theorem which tells us that $bas{{e}^{2}}+heigh{{t}^{2}}=hypotenus{{e}^{2}}$
So,
$\begin{align}
  & A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \\
 & \Rightarrow AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}} \\
\end{align}$
So, $AC=\sqrt{{{\left( 1.6 \right)}^{2}}+{{\left( 2.8 \right)}^{2}}}=\sqrt{2.56+7.84}=3.22$
Then using the inverse formula, we will find the value of $\angle BAC$.
Also, we need to remember that the exact solution for $\alpha ={{\tan }^{-1}}\left( \dfrac{7}{4} \right)$ will be taken into consideration not the general solution as $\alpha \in \left( 0,\pi \right)$.
So, $\alpha ={{\tan }^{-1}}\left( \dfrac{7}{4} \right)={{60.25}^{\circ }}$(approximation).