
Can two angles be supplementary without being a linear pair. Give a few examples?
Answer
477.6k+ views
Hint: Two angles are said to be supplementary angles if their sum is equal to \[{180^ \circ }\]. A Linear Pair Is formed when two lines intersect each other at a common point and they are adjacent to each other. We know, a linear pair forms a pair of supplementary angles but we have to find the supplementary angles which do not form a linear pair.
Complete step-by-step answer:
Let us First see what a linear pair is through a diagram.
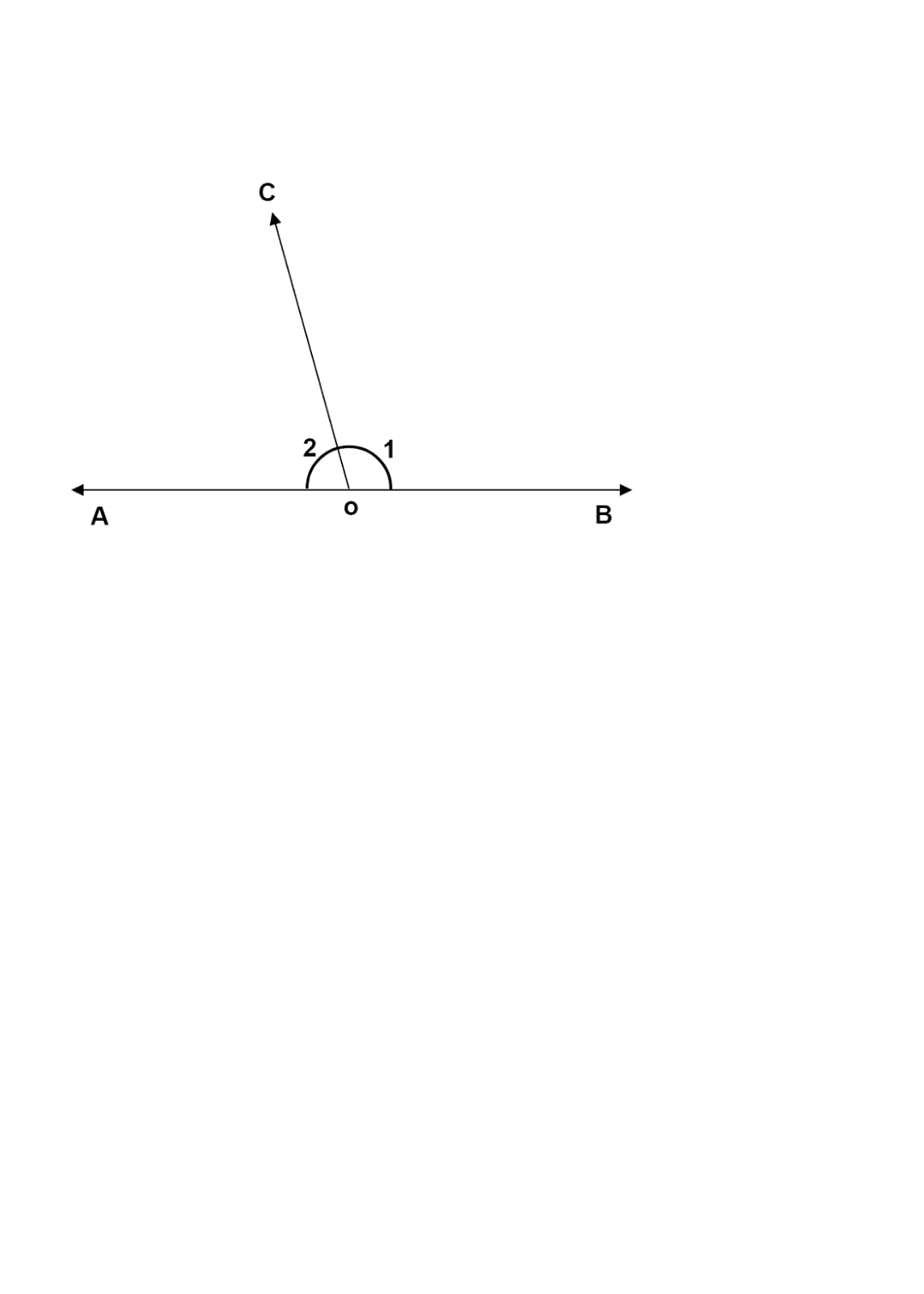
Here \[\angle 1\] and \[\angle 2\] form a linear pair as they are adjacent to each other and here the line \[AB\] and ray \[OC\] intersect at \[O\].
Now, let us look at some other examples where two angles are supplementary angles but they do not form a linear pair.
Let us consider two parallel lines \[m\] and \[n\], and \[l\] be a transversal.

Here, \[\angle 4\] and \[\angle 5\] are together known as co-interior angles and their sum is equal to \[{180^ \circ }\]. So, they form a pair of supplementary angles. Similarly, \[\angle 3\] and \[\angle 6\] are also called co-interior angles and their sum is also equal to \[{180^ \circ }\]. Also, they do not form a linear pair.
So, we can say that co-interior angles between two parallel lines are supplementary angles.
Now, let us consider a cyclic quadrilateral. i.e. a quadrilateral whose all vertices lie on a circle circumscribing the quadrilateral.
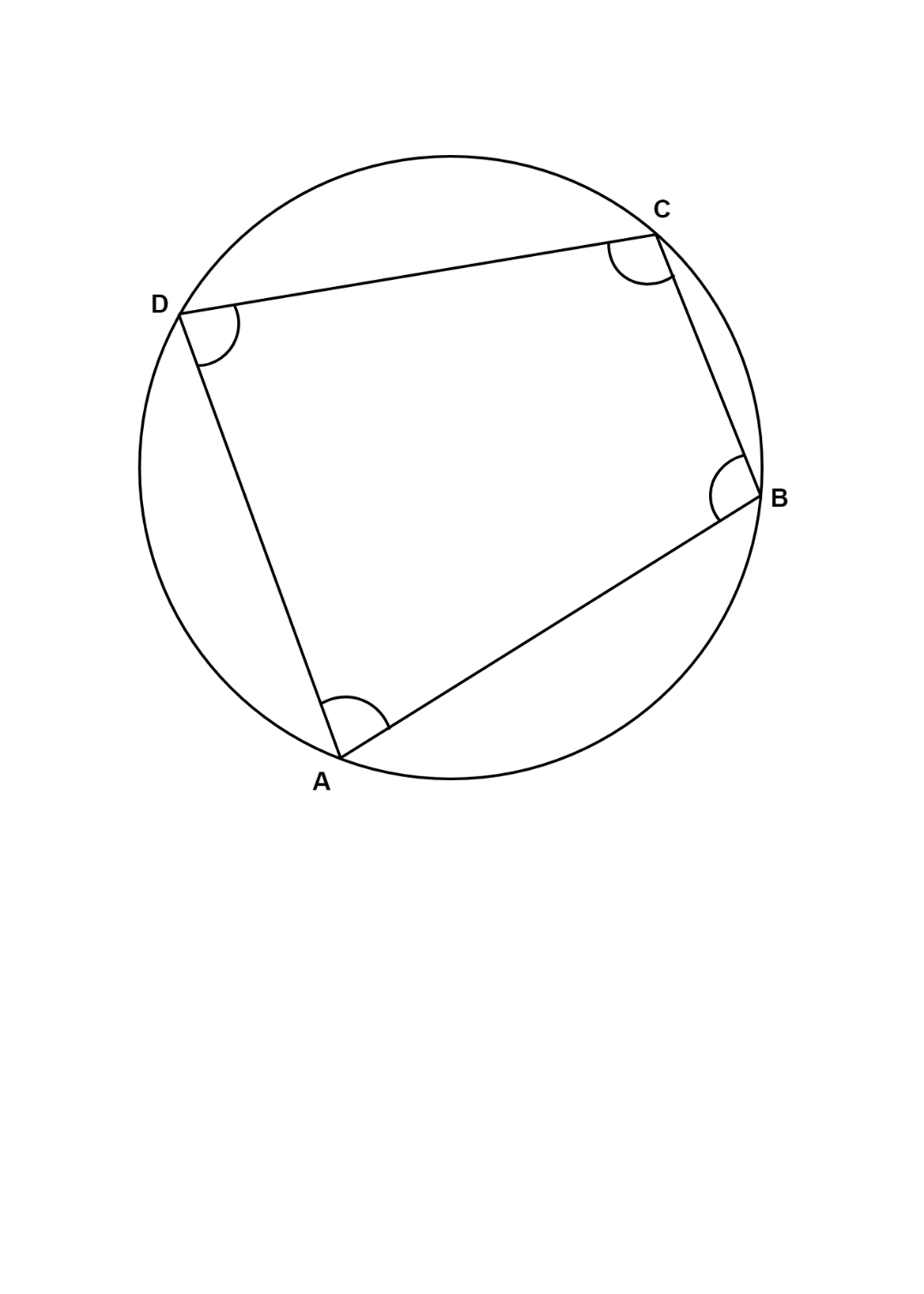
In this cyclic quadrilateral, the opposite angles, i.e. \[\angle A\] and \[\angle C\] form a pair of supplementary angles and they are not linear pairs as well. Similarly, \[\angle B\] and \[\angle D\] also form a pair of supplementary angles which are not linear pairs.
Hence, we can say that Two angles can be supplementary being a linear pair.
Note: For such types of questions, we need to be very clear with the definitions of every term. Some people get confused between linear pair and supplementary angles and consider that it is a necessary condition for supplementary angles to form a linear pair but they both are different things and we can compare their definitions as well as these things can be best understood using a diagram. Not only these two examples provided above satisfy this but we can find many other examples as well.
Complete step-by-step answer:
Let us First see what a linear pair is through a diagram.

Here \[\angle 1\] and \[\angle 2\] form a linear pair as they are adjacent to each other and here the line \[AB\] and ray \[OC\] intersect at \[O\].
Now, let us look at some other examples where two angles are supplementary angles but they do not form a linear pair.
Let us consider two parallel lines \[m\] and \[n\], and \[l\] be a transversal.

Here, \[\angle 4\] and \[\angle 5\] are together known as co-interior angles and their sum is equal to \[{180^ \circ }\]. So, they form a pair of supplementary angles. Similarly, \[\angle 3\] and \[\angle 6\] are also called co-interior angles and their sum is also equal to \[{180^ \circ }\]. Also, they do not form a linear pair.
So, we can say that co-interior angles between two parallel lines are supplementary angles.
Now, let us consider a cyclic quadrilateral. i.e. a quadrilateral whose all vertices lie on a circle circumscribing the quadrilateral.

In this cyclic quadrilateral, the opposite angles, i.e. \[\angle A\] and \[\angle C\] form a pair of supplementary angles and they are not linear pairs as well. Similarly, \[\angle B\] and \[\angle D\] also form a pair of supplementary angles which are not linear pairs.
Hence, we can say that Two angles can be supplementary being a linear pair.
Note: For such types of questions, we need to be very clear with the definitions of every term. Some people get confused between linear pair and supplementary angles and consider that it is a necessary condition for supplementary angles to form a linear pair but they both are different things and we can compare their definitions as well as these things can be best understood using a diagram. Not only these two examples provided above satisfy this but we can find many other examples as well.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

What are gulf countries and why they are called Gulf class 8 social science CBSE





