Question

Can we have a triangle having sides 4cm, 8cm and 3cm?

Answer 1

Hint: We will start by using one of the triangle's characteristics, which states that the sum of the lengths of any two of the triangle's sides should always be larger than the length of the third side. To make the triangle, the sides should satisfy all 3 inequalities.

Complete step by step answer:
We will see the property of the triangle that states that: The total of the lengths of any two triangle sides should always be more than the length of the third side, according to the triangle's property.

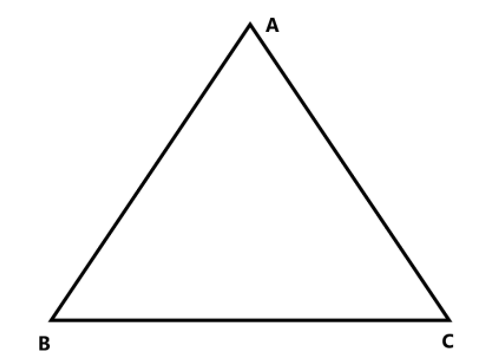
All of the inequalities listed below must be satisfied for any triangle ABC:
\[AB + BC > AC\] (1)
\[AB + AC > BC\] (2)
$BC + AC > AB$ (3)
Now we must determine whether a triangle can be formed with sides of 4cm, 8cm, and 3cm in length.
We will assume that AB is 4 cm, BC is 8 cm, and AC is 3 cm. Now we'll see if all three of the previously specified inequalities are met or not.
\[AB + BC{\text{ = 4 + 8}} = 12cm\] and $AC = 3cm$
we can see that the inequality \[AB + BC > AC\] is satisfied.
we will now see second inequality
\[AB + AC = 4 + 3 = 7cm\] and \[BC = 8cm\]
we can see the inequality \[AB + AC > BC\] is not satisfied.
Since the second inequality is not satisfied, we will not check further.
Therefore, the triangle having sides 4cm, 8cm and 3cm is not possible.

Note:The supplied sides in this issue do not form any kind of triangle. However, if the sides are such that the sum of the lengths of any two sides is greater than the length of the triangle's third side, the triangle is formed, and the triangle can be classified as scalene, isosceles, or equilateral depending on the lengths of the sides.