Question

What is centripetal acceleration? Derive the expression for centripetal acceleration.

Answer 1

Hint: In circular motion centripetal force is perpendicular to velocity. Also if the particles decrease or increase their speeds in circular motion then acceleration is generated which deviates the net acceleration from pointing towards the centre.
Formula used:
$a=\dfrac{v^{2}}{r}$

Complete answer:
We know that the motions are two types: one is straight motion and the circular motion. Then we know that circular motion, though the magnitude of velocity is a constant, the direction of velocity is changing. A circle. It is also defined as rotation of an object along a circular path. It can be of two forms, uniform circular motion, with constant angular rate of rotation and constant speed, or non-uniform circular motion with a changing rate of rotation.

Consider a body of mass $m$ moving along the circumference of a circle. the radius of a circle $r$ with velocity $v$,as shown in the figure. Then if a small force $F$ is applied on the body, then we know that the force is given as $F=ma$.

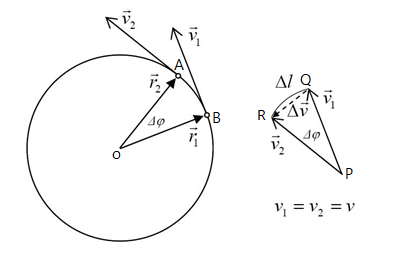
Where, $a$ is the acceleration and is given as the rate of change of velocity $\Delta v$ with respect to time.
Consider the \[\vartriangle OAB\] and $\triangle PQR$, then $\dfrac{\Delta v}{AB}=\dfrac{v}{r}$
Clearly, $AB=v\Delta t$
$\implies \dfrac{\Delta v}{v\Delta t}=\dfrac{v}{r}$
$\implies \dfrac{\Delta v}{\Delta t}=\dfrac{v^{2}}{r}$
$\implies a=\dfrac{v^{2}}{r}$

Thus, the acceleration due to centripetal force is given by,$a=\dfrac{v^{2}}{r}$. Clearly as the velocity $v$ and the radius $r$ of the circle are constant, acceleration $a$ will also remain a constant.

Note:
Centripetal force is the force that acts on a body moving in a circular path and is directed towards the centre around which the body is moving. If the particles decrease or increase their speeds during the circular motion the net force deviates the particle from its initial path.