Question

Circle ${{x}^{2}}+{{y}^{2}}+6y=0$ touches \[\]
A. $y-$axis at the origin\[\]
B. $x-$axis at the origin\[\]
C. $x-$axis at the point $\left( 3,0 \right)$\[\]
D. The line $y+3=0$\[\]

Answer 1

Hint: We convert the given equation to the centre –radius from of equation of general circle ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ to find the centre $\left( a,b \right)$ and radius $r$. We use the perpendicular distance between a point $\left( {{x}_{1}},{{y}_{1}} \right)$ from a line $ax+by+c=0$ which is given by $d=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ to find the distance from the centre to the tangent line and check that is equal to the radius. If it is equal it is a tangent otherwise it is not. \[\]

Complete step by step answer:
Let us convert the given equation of circle ${{x}^{2}}+{{y}^{2}}+6y=0$ into centre-radius form using the completing square method. We have;
\[\begin{align}
  & {{x}^{2}}+{{y}^{2}}+6y=0 \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}+2\cdot 3\cdot y+{{3}^{2}}={{3}^{2}} \\
 & \Rightarrow {{x}^{2}}+{{\left( y+3 \right)}^{2}}={{3}^{2}} \\
 & \Rightarrow {{\left( x-0 \right)}^{2}}+{{\left( y-\left( -3 \right) \right)}^{2}}={{3}^{2}} \\
\end{align}\]
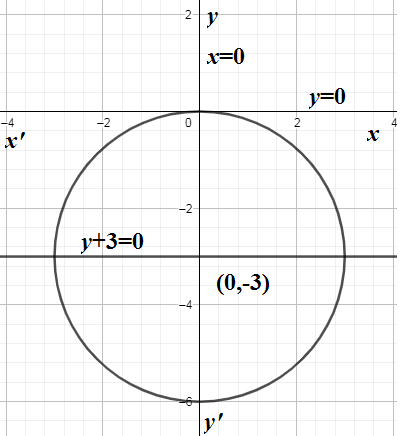
We obtain the centre of the given circle as $\left( 0,-3 \right)$ and radius 3.
Let us check each option.\[\]
(A)We know that the equation of the $y-$axis is $x=0$. So the distance of the centre $\left( 0,-3 \right)$ from the $y-$axis is
\[d=\dfrac{\left| 1\cdot 0 \right|}{\sqrt{{{1}^{2}}}}=0\]
Since distance is not equal to radius, $y-$axis does not touch the circle. \[\]
(B) We know that the equation of the $x-$axis is $y=0$. So the distance of the centre $\left( 0,-3 \right)$ from the $x-$axis is
 \[d=\dfrac{\left| -3\cdot 1 \right|}{\sqrt{{{1}^{2}}}}=3\]
Since distance is equal to radius, $x-$axis touches the circle.\[\]
 (C)Since the point of contact of a circle and a tangent is unique $x-$axis, we put $y=0$ in the equation of circle to have;
\[\begin{align}
  & {{x}^{2}}=0 \\
 & \Rightarrow x=0 \\
\end{align}\]
So the point of contact is origin $\left( 0,0 \right)$ not $\left( 3,0 \right)$. \[\]
(D)We are given the equation of line $y+3=0$. So the distance of the centre $\left( 0,-3 \right)$ from the line $y+3=0$ is
\[d=\dfrac{\left| -3\cdot 1+3 \right|}{\sqrt{{{1}^{2}}}}=0\]
 Since distance is not equal to radius, the line $y+3=0$ does not touch the circle. \[\]

So, the correct answer is “Option B”.

Note: We can directly use the fact that a circle touching $x-$axis will have the absolute value of $y-$coordinate of the centre equal to the length of the radius and similarly a circle touching $y-$axis will have the absolute value of $x-$coordinate of the centre equal to the length of the radius. We can also use the fact that the centre lies on the $y-$axis and the line $y+3=0$ to discard options A and D.