
Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment

Answer
504k+ views
4 likes
Hint: In this particular question first, draw perpendicular lines of unit (i.e. 1) length and then join their end point with O. And will apply Pythagoras Theorem (i.e.
Complete step-by-step answer:
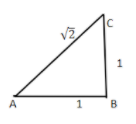
So, let us first draw a line segment AB of unit length.
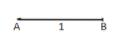
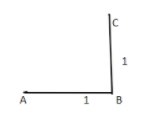
Then draw a line BC that is perpendicular to the line AB and is of unit length.
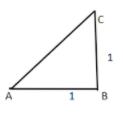
Now we had to join point A with point C.
Now as we know that
So, according to Pythagoras theorem
So, in triangle ABC
Now draw a line CD that is perpendicular to the line CA and is of unit length.
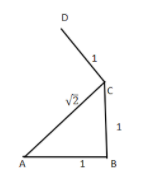
Join point D with point A.
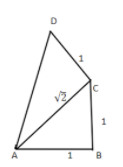
Now again applying Pythagoras theorem in triangle ACD.
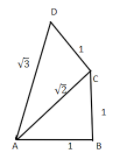
Similarly, proceeding further each time we will get a line having length equal to the square root of a next natural number.
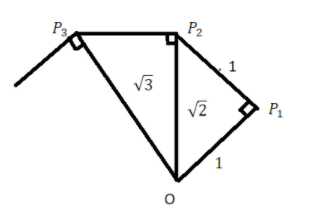
So, the square root spiral will be as follows
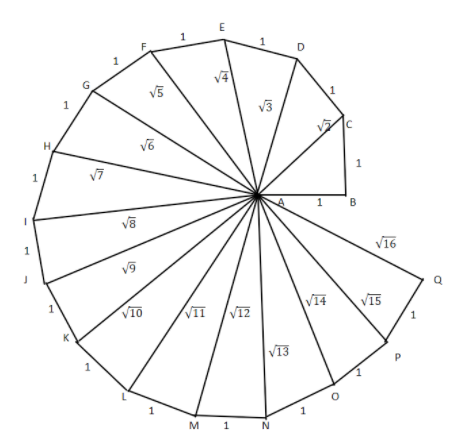
Note:Whenever we face such types of questions the key concept we have to remember is that each time the length of the new line formed is the square root of the next natural number than the previous one because the new line formed is the hypotenuse of the new triangle. And the base the previous line while the perpendicular is always of unit length. So, by Pythagoras theorem
Complete step-by-step answer:
So, let us first draw a line segment AB of unit length.
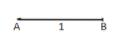
Then draw a line BC that is perpendicular to the line AB and is of unit length.

Now we had to join point A with point C.

Now as we know that
So, according to Pythagoras theorem
So, in triangle ABC

Now draw a line CD that is perpendicular to the line CA and is of unit length.

Join point D with point A.

Now again applying Pythagoras theorem in triangle ACD.

Similarly, proceeding further each time we will get a line having length equal to the square root of a next natural number.
So, the square root spiral will be as follows

Note:Whenever we face such types of questions the key concept we have to remember is that each time the length of the new line formed is the square root of the next natural number than the previous one because the new line formed is the hypotenuse of the new triangle. And the base the previous line while the perpendicular is always of unit length. So, by Pythagoras theorem
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
List some examples of Rabi and Kharif crops class 8 biology CBSE

How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

Advantages and disadvantages of science

10 slogans on organ donation class 8 english CBSE




