Question

How can you combine three resistances, each of \[4\Omega \], such that the total resistance of the circuit is \[6\Omega \]?(Draw Circuit)

Answer 1

Hint: This question is based on a combination of resistors, there are two types of combination Series and parallel. A circuit is said to be connected in series when the same amount of current flows through the resistors. And A circuit is said to be connected in parallel when the voltage is the same across the resistors.
Formula Used: \[R{}_{eq} = \,R{}_1 + {R_2} + {R_{3.........}}\] (for series) and \[R{}_{eq} = \,\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}........\] (for parallel).

Complete step-by-step solution:
To get an equivalent resistance of \[6\Omega \], we have to use both parallel and series combinations in the circuit.
First, the two resistors are connected in parallel combination to obtain equivalent resistance of \[2\Omega \]
Then the combined resistance (of \[2\Omega \]) in series this will give total resistance equal to \[6\Omega \]
That is,
\[ R{}_{eq} = \,\dfrac{1}{4} + \dfrac{1}{4} \\
   \Rightarrow \dfrac{2}{4} = \dfrac{1}{2} \\
   \Rightarrow {R_{eq}} = 2\,\Omega \]
Now this equivalent resistance of \[2\Omega \] is connected in series with the third \[4\Omega \],
\[ {R_{eq}} = 2\,\Omega + 4\,\Omega \\
  {R_{eq}} = 6\,\Omega \]
When we draw a diagram of this, we get,

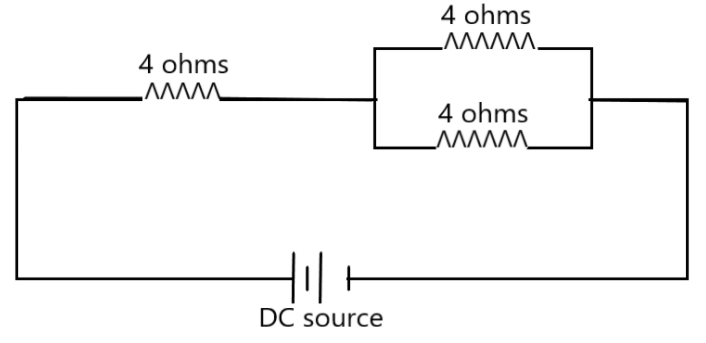
That is, for the two resistors in parallel the resistance is given as \[2\Omega \] and this is added with the resistance of the third resistor in the series as \[6\Omega \].

Note: Always remember that in series combination equivalent resistance comes out to be more than magnitude of single component resistor and in parallel equivalent resistance comes out to be less than that of magnitude of single component resistor.