Question

Compare, giving reasons, the J-shaped and S-shaped models of population growth of a species.

Answer 1

Hint: The J-shaped curve is seen in the case when there are unlimited resources in the environment but the S-shaped curve is seen when the resources are limited. Also, the second one involves a stationary phase which is not a part of the first one.

Complete answer:
The J-shaped curve is obtained in the case of exponential growth. For this type of growth, the suitable condition is the availability of unlimited resources in the environment in which the population lives. Here, the unlimited resources mean unlimited food and land so that the population can grow with its maximum fertility capacity. This is practically not possible because in our environment the resources are not limited for any population or species. This is the reason that this type of growth curve is shown only by the microorganisms that are grown in the culture media with the unlimited supply of nutrients. A J-shaped growth curve has been shown below –

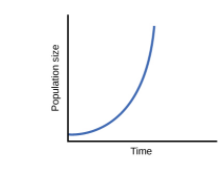
The S-shaped curve is obtained in the case of logistic growth. This type of growth curve is more practical than the J-shaped and is shown by the organisms living in a natural environment. As the resources are limited in the environment, the growth rate varies with respect to time. Initially, the growth is comparatively slower but later it shows a sharp increase and when it reaches near the carrying capacity of the environment, it becomes too slow because at this point the population has consumed maximum available resources. An S-shaped curve looks like –

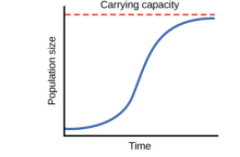
Note:There are two phases in the exponential growth, first one is the lag phase and the second one is the log phase but in the logistic growth, there are four phases as lag phase, log phase, deceleration phase, and stationary phase.
>Carrying capacity of the environment is not considered in the case of exponential growth but it serves as an important factor in the case of logistic growth.