Question

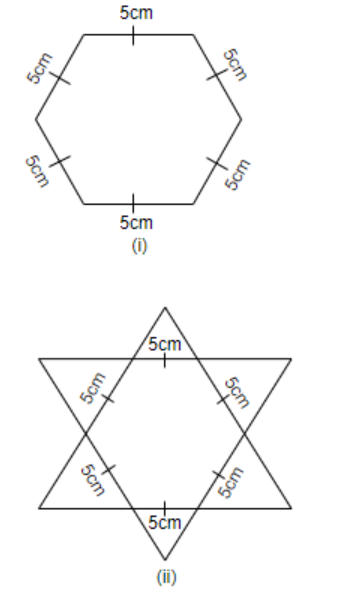
Complete the hexagonal and star shaped Rangolies [see fig. (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

Answer 1

Hint: We will find the number of equilateral triangles formed in the hexagonal and star shaped rangolis given. Then, we will find the area of both the rangolis individually. For this we will find the area of the equilateral triangles of 5cm and then multiply it with the number of equilateral triangles in the hexagona and star shaped rangolis individually. The number of equilateral triangles of 1 cm can be calculated as, $\dfrac{\text{Area of hexagonal or star shaped rangoli}}{\text{Area of 1 equilateral triangle of side 1cm}}$. And area of an equilateral triangle is given by, $\dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}}$

Complete step-by-step answer:
It is given in the question that we have to complete hexagonal and star shaped Rangolis by filling them with as many equilateral triangles of side 1 cm as we can. And we have to count the number of triangles in each case and find out which has more number of triangles.
Now, we will consider figure (i), that is the hexagonal shaped rangoli and we will construct equilateral triangles inside it. And we will name the hexagon as ABCDEF, so, we will get the figure as follows.

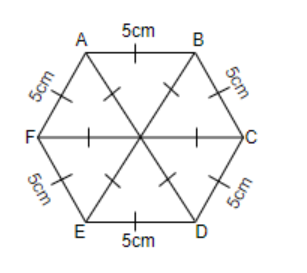
So, we can see that there are 6 equilateral triangles of side 5cm each that can be drawn for the hexagon.
We know that the area of the equilateral triangle = $\dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}}$.
So, the area of 1 equilateral triangle, say, triangle OAB of side 5cm will be,
$\begin{align}
  & \dfrac{\sqrt{3}}{4}{{\left( 5 \right)}^{2}} \\
 & \dfrac{\sqrt{3}}{4}\times 25 \\
 & \dfrac{25\sqrt{3}}{4}c{{m}^{2}} \\
\end{align}$
Thus, area of each equilateral triangle will be $\dfrac{25\sqrt{3}}{4}c{{m}^{2}}$ as all the equilateral triangles are equal having the side as 5cm.
Therefore, we get the area of the hexagon as, $6\times \text{area of 1 equilateral triangle of side 5cm}$
$\begin{align}
  & =6\times \dfrac{25\sqrt{3}}{4} \\
 & =\dfrac{150\sqrt{3}}{4}c{{m}^{2}} \\
\end{align}$
Now, the area of equilateral triangle of side 1cm, will be $\dfrac{\sqrt{3}}{4}\times {{\left( 1 \right)}^{2}}=\dfrac{\sqrt{3}}{4}c{{m}^{2}}$.
So, the number of equilateral triangles of side 1cm in the hexagon ABCDEF will be,
$\dfrac{\text{Area of hexagon}}{\text{Area of 1 equilateral triangle of side 1cm}}$
We have the area of the hexagon as $\dfrac{150\sqrt{3}}{4}c{{m}^{2}}$ and the area of an equilateral triangle of side 1cm as $\dfrac{\sqrt{3}}{4}c{{m}^{2}}$.
On substituting these values in the equation, we get,
$\begin{align}
  & \dfrac{\dfrac{150\sqrt{3}}{4}}{\dfrac{\sqrt{3}}{4}} \\
 & =\dfrac{150\sqrt{3}}{4}\times \dfrac{4}{\sqrt{3}} \\
 & =150 \\
\end{align}$
Hence, there will be 150 equilateral triangles of side 1cm each in the hexagonal shaped rangoli.
Now, let us consider figure (ii), that is the star shaped rangoli.
So, here also, we will draw the possible equilateral triangles in the figure, so we will get,

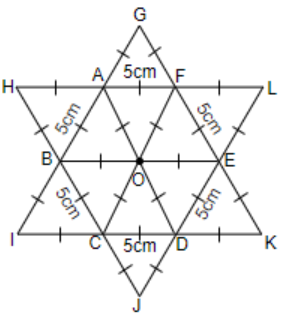
So, we can see that ABCDEF is a hexagon of side 5cm, so there will be 6 equilateral triangles of side 5cm formed in the hexagon, also we have an additional 6 equilateral triangles of side 5cm in the figure. So, there are a total of (6 + 6) = 12 equilateral triangles in the figure.
Now, we know that area of an equilateral triangle of side 5cm will be,
$\begin{align}
  & \dfrac{\sqrt{3}}{4}{{\left( 5 \right)}^{2}} \\
 & \dfrac{\sqrt{3}}{4}\times 25 \\
 & \dfrac{25\sqrt{3}}{4}c{{m}^{2}} \\
\end{align}$
Thus, each equilateral triangle of side 5cm in the figure, will have the area as $\dfrac{25\sqrt{3}}{4}c{{m}^{2}}$.
So, the area of the rangoli will be,
$\begin{align}
  & =12\times \dfrac{25\sqrt{3}}{4} \\
 & =\dfrac{300\sqrt{3}}{4}c{{m}^{2}} \\
\end{align}$
Now, the area of equilateral triangle of side 1cm, will be $\dfrac{\sqrt{3}}{4}\times {{\left( 1 \right)}^{2}}=\dfrac{\sqrt{3}}{4}c{{m}^{2}}$.
So, the number of equilateral triangles of side 1cm in the hexagon ABCDEF will be,
$\dfrac{\text{Area of star shaped rangoli}}{\text{Area of 1 equilateral triangle of side 1cm}}$
We have the area of the hexagon as $\dfrac{300\sqrt{3}}{4}c{{m}^{2}}$ and the area of an equilateral triangle of side 1cm as $\dfrac{\sqrt{3}}{4}c{{m}^{2}}$.
On substituting these values in the equation, we get,
$\begin{align}
  & \dfrac{\dfrac{300\sqrt{3}}{4}}{\dfrac{\sqrt{3}}{4}} \\
 & =\dfrac{300\sqrt{3}}{4}\times \dfrac{4}{\sqrt{3}} \\
 & =300 \\
\end{align}$
Hence, there will be 300 equilateral triangles of side 1cm each in the star shaped rangoli.
Therefore, from the solution, it is clear that the star shaped rangoli has more number of equilateral triangles of side 1 cm than the hexagonal shaped rangoli.

Note: Many students make a mistake by literally counting the number of equilateral triangles of side 1cm from the figure, but this is not possible, hence it is recommended that the students follow the conventional method to solve this question. Also, while filling the equilateral triangles in the hexagonal or star shaped rangolis, they may draw more number of triangles than required, but that will be wrong as all the triangles won’t be equilateral and will not be of sides 5cm. For example, some students may draw the hexagonal rangoli as follows.

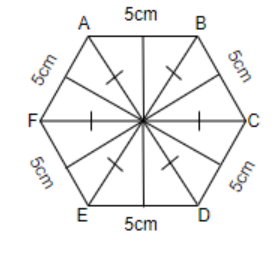
But this is wrong as few of the triangles are right angle triangles and not equilateral, so the students must be careful while solving this question.