Question

Concentric circles of radii 1, 2, 3, …, 100 cm are drawn. The interior of the smallest circle is coloured red and the angular regions are coloured alternatively green and red, so that no two adjacent regions are of the same colour. The total area of the green region in sq. cm is equal to
(a) \[1000\pi \]
(b) \[5050\pi \]
(c) \[4950\pi \]
(d) \[5151\pi \]

Answer 1

Hint: We solve this problem by using the formula of area of circle.
The formula of area of circle having the radius \[r\] is given as
\[A=\pi {{r}^{2}}\]
We also have the formula of summation of squares of first \[n\] natural numbers is given as
\[{{1}^{2}}+{{2}^{2}}+{{3}^{2}}+....+{{n}^{2}}=\dfrac{n\left( n+1 \right)\left( 2n+1 \right)}{6}\]

Complete answer:
Let us take a rough figure of the given circles as follows

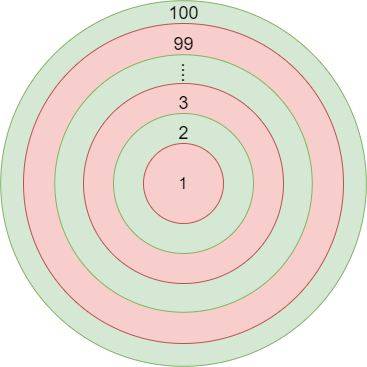
Here, we can see that circles of odd radii are red colour and circles of even radii are green in colour.
We are asked to find the total area of the green region.
Let us assume that the area of first green region that is 2 as \[{{A}_{1}}\]
We know that the formula of area of circle having the radius \[r\] is given as
\[A=\pi {{r}^{2}}\]
By using the above formula we get the area of first green region as
\[\begin{align}
  & \Rightarrow {{A}_{1}}=\pi \left( {{2}^{2}} \right)-\pi \left( {{1}^{2}} \right) \\
 & \Rightarrow {{A}_{1}}=\pi \left( {{2}^{2}}-{{1}^{2}} \right) \\
\end{align}\]
Now, let us assume that the area of next green region as \[{{A}_{2}}\]
By using the area of circle formula we get
\[\Rightarrow {{A}_{2}}=\pi \left( {{4}^{2}}-{{3}^{2}} \right)\]
Let us assume that the total area of the green region as \[A\] then we get
\[\begin{align}
  & \Rightarrow A={{A}_{1}}+{{A}_{2}}+.....+{{A}_{n}} \\
 & \Rightarrow A=\pi \left( {{2}^{2}}-{{1}^{2}} \right)+\pi \left( {{4}^{2}}-{{3}^{2}} \right)+....+\pi \left( {{100}^{2}}-{{99}^{2}} \right) \\
\end{align}\]
Now, let us divide the terms of even and odd terms separately then we get
\[\Rightarrow A=\pi \left( {{2}^{2}}+{{4}^{2}}+....+{{100}^{2}} \right)-\pi \left( {{1}^{2}}+{{3}^{2}}+....+{{99}^{2}} \right)\]
Now, let us add and subtract the even terms in the above equation then we get
\[\begin{align}
  & \Rightarrow A=2\pi \left( {{2}^{2}}+{{4}^{2}}+....+{{100}^{2}} \right)-\pi \left( {{1}^{2}}+{{2}^{2}}+{{3}^{2}}+.....+{{99}^{2}}+{{100}^{2}} \right) \\
 & \Rightarrow A=2\pi \times {{2}^{2}}\left( {{1}^{2}}+{{2}^{2}}+.....+{{50}^{2}} \right)-\pi \left( {{1}^{2}}+{{2}^{2}}+....+{{100}^{2}} \right) \\
 & \Rightarrow A=8\pi \left( {{1}^{2}}+{{2}^{2}}+.....+{{50}^{2}} \right)-\pi \left( {{1}^{2}}+{{2}^{2}}+....+{{100}^{2}} \right) \\
\end{align}\]
We know that the formula of summation of squares of first \[n\] natural numbers is given as
\[{{1}^{2}}+{{2}^{2}}+{{3}^{2}}+....+{{n}^{2}}=\dfrac{n\left( n+1 \right)\left( 2n+1 \right)}{6}\]
By using this formula of sum of square of numbers in above equation then we get
\[\Rightarrow A=8\pi \left( \dfrac{50\left( 50+1 \right)\left( 2\times 50+1 \right)}{6} \right)-\pi \left( \dfrac{100\left( 100+1 \right)\left( 2\times 100+1 \right)}{6} \right)\]
\[\Rightarrow A=8\pi \left( \dfrac{50\times 51\times 101}{6} \right)-\pi \left( \dfrac{100\times 101\times 201}{6} \right)\]
Now, let us take the common terms out from both terms then we get
\[\begin{align}
  & \Rightarrow A=\left( \dfrac{101\pi }{6} \right)\left( \left( 8\times 50\times 51 \right)-\left( 100\times 201 \right) \right) \\
 & \Rightarrow A=\left( \dfrac{101\pi }{6} \right)\left( 20400-20100 \right) \\
 & \Rightarrow A=\dfrac{101\pi \times 300}{6}=5050\pi \\
\end{align}\]
Therefore we can conclude that the area of green region is \[5050\pi \] sq. cm

So, option (b) is the correct answer.

Note:
Students may make mistakes in taking the area of the green region.
Here, we can see that the green region is not a complete circle which is the region.
The area of green region is obtained by difference of areas of two consecutive circles that is
\[\Rightarrow A=\pi \left( {{2}^{2}}-{{1}^{2}} \right)+\pi \left( {{4}^{2}}-{{3}^{2}} \right)+....+\pi \left( {{100}^{2}}-{{99}^{2}} \right)\]
But students may make mistakes when considering the figure.
They assume that the each region is a complete circle and take the equation as
\[\Rightarrow A=\pi \left( {{2}^{2}} \right)+\pi \left( {{4}^{2}} \right)+....+\pi \left( {{100}^{2}} \right)\]
This gives the wrong answer.